Haben Sie sich jemals gefragt, warum sich manche Federn beim Zusammendrücken “steifer” anfühlen, während andere über ihren gesamten Federweg einen gleichmäßigen Widerstand beibehalten? Oder warum bestimmte industrielle Anwendungen Federn mit ganz spezifischen Last-Verformungs-Eigenschaften erfordern? Die Antwort liegt im Verständnis Federkennlinien Und Steifheit—zwei grundlegende Konzepte, die jeder Ingenieur, Designer und Beschaffungsspezialist beherrschen sollte.
In diesem umfassenden Leitfaden gehen wir detailliert auf die wissenschaftlichen Grundlagen von Federkennlinien ein, untersuchen die verschiedenen Kennlinientypen und ihre praktischen Auswirkungen und helfen Ihnen, die richtige Feder für Ihre spezifische Anwendung auszuwählen. Ob Sie Formensysteme, Fahrzeugfederungen oder Präzisionselektronik entwickeln – dieses Wissen ist von unschätzbarem Wert.
Kurzantwort (60 Sekunden)
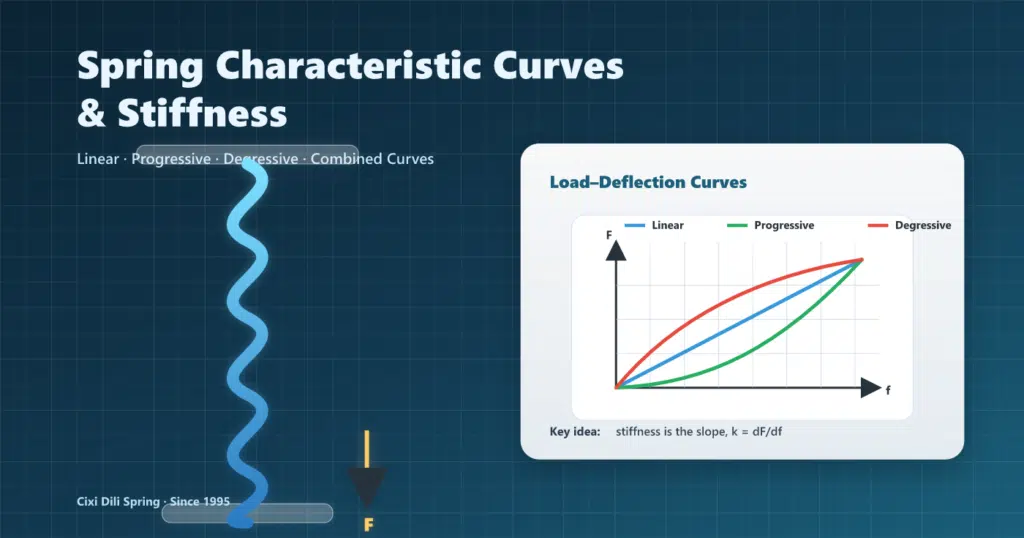
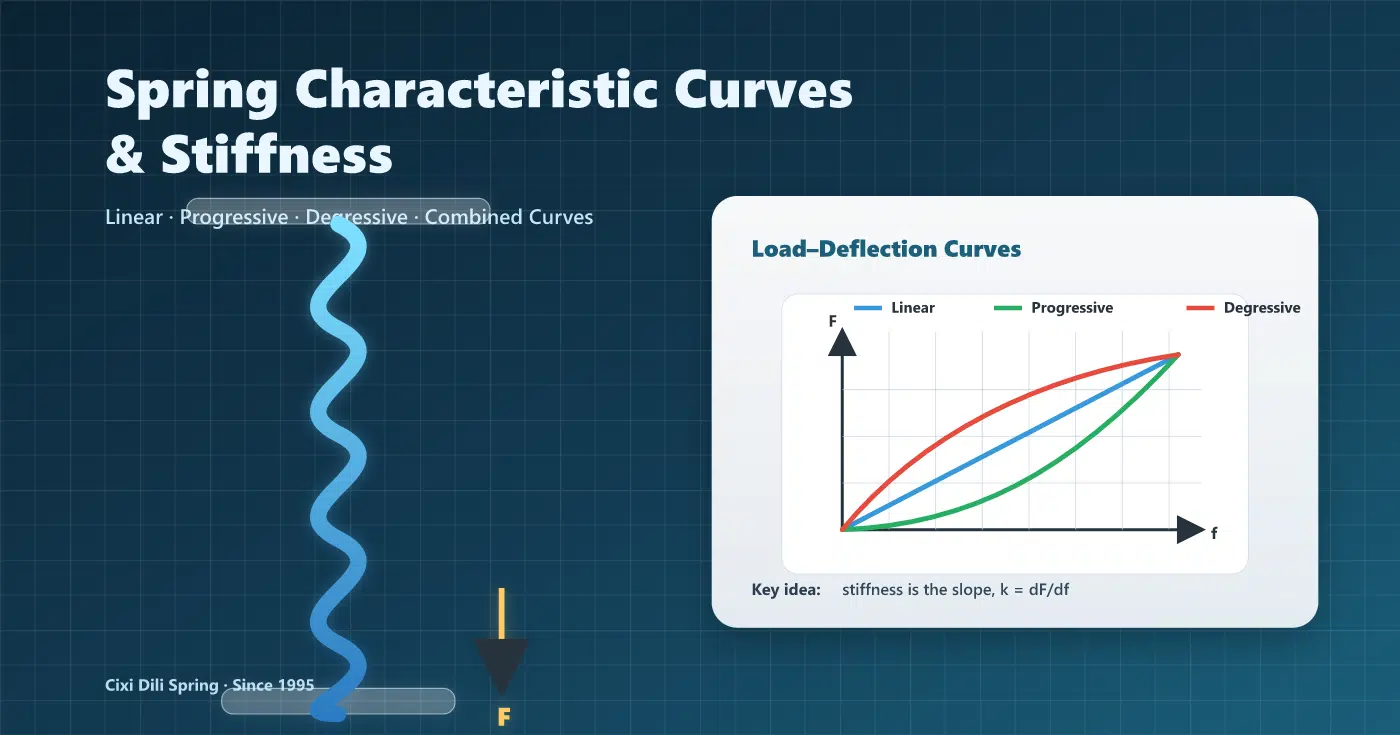
- Federkennlinie = die Kraft-Auslenkungs- (F-f) oder Drehmoment-Winkel-Beziehung (T-φ).
- Steifigkeit / Federrate An einem Punkt entspricht die Kurvensteigung: k = dF/df (oder kθ = dT/dφ).
- Linear: k Konstante. Progressiv: k nimmt mit der Auslenkung zu. Degressiv: k nimmt mit zunehmender Auslenkung ab.
- Bei nichtlinearen Kurven ist zu unterscheiden Tangentensteifigkeit (dF/df) vs Sekantensteifigkeit (F/f) am Arbeitspunkt.
Inhaltsverzeichnis
- Was sind Federkennlinien?
- Drei Arten von Fundamentalkurven
- Kombinierte und komplexe Kurven
- Federsteifigkeit und Federrate
- Wie Kurven die Auswahl beeinflussen
- Ein praktischer Auswahlrahmen
- Praktische Überlegungen
- Warum eine Partnerschaft mit einem Hersteller eingehen?
- Abschluss
- FAQs
Was sind Federkennlinien?
A Federkennlinie stellt die Beziehung zwischen der Last (Kraft) dar F oder Drehmoment Tangewendet auf eine Feder und die daraus resultierende Verformung (Auslenkung) f oder Winkelverschiebung φVereinfacht ausgedrückt handelt es sich um eine grafische Darstellung, wie eine Feder auf zunehmende Belastungen reagiert.
Stellen Sie es sich so vor: Wenn Sie eine Feder mit der Hand zusammendrücken und sowohl die aufgewendete Kraft als auch die Kompression der Feder messen, erhalten Sie durch das Tragen dieser Werte in ein Diagramm eine Kennlinie. Diese Kennlinie beschreibt das Verhalten der Feder unter Belastung vollständig.
Warum sind charakteristische Kurven wichtig?
Das Verständnis von Charakteristikkurven ist aus mehreren Gründen von entscheidender Bedeutung:
- Vorhersagbare LeistungIngenieure können genau vorhersagen, wie sich eine Feder in einer bestimmten Anwendung verhalten wird.
- LastmanagementDie Kenntnis der Kurve hilft bei der Entwicklung von Systemen, die Lasten effektiv verwalten.
- SicherheitsüberlegungenKritische Anwendungen erfordern präzise Kenntnisse über das Verhalten von Federn unter extremen Bedingungen.
- KostenoptimierungDie Wahl des richtigen Federtyps reduziert Überdimensionierung und unnötige Kosten.
Bei Cixi Dili Spring Co., Ltd., Wir stellen seit 1995 Federn her und können Ihnen aus Erfahrung sagen, dass das Verständnis dieser Kurven oft den Unterschied zwischen einer erfolgreichen Anwendung und einem kostspieligen Fehlschlag ausmacht.
Die drei grundlegenden Arten von Federkennlinien
Die Kennlinien von Federn lassen sich grob in drei Grundtypen einteilen, von denen jeder ein bestimmtes Verhalten und Anwendungsgebiet aufweist.
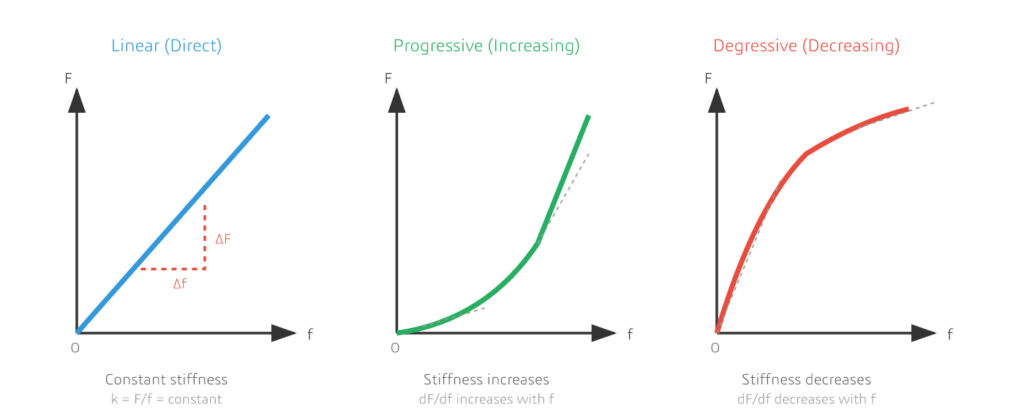
Abbildung 2: Die drei grundlegenden Arten von Federkennlinien – linear, progressiv (steigend) und degressiv (fallend)
| Kurventyp | Was geschieht mit der Steifigkeit (k)? | Typische Designs | Am besten geeignet für |
|---|---|---|---|
| Linear | Konstante: k = dF/df ist im gesamten Arbeitsbereich gleich | Die meisten Schraubendruck-/Zugfedern, Standard-Druckfedern | Vorhersagbare Kraft in jeder Position, einfache Dimensionierung und Steuerung |
| Progressiv | Zunahme: k wächst mit zunehmender Auslenkung | Variable Steigung, konische Federn, Konstruktionen, die die Windungen in Kontakt bringen | Sanftes Ansprechverhalten, Überlast-/Durchschlagsfestigkeit |
| Degressiv | Abnehmend: k sinkt mit zunehmender Auslenkung | Spezielle Geometrien/Materialsysteme; einige Federstapel | Hoher anfänglicher Widerstand mit schwächerer Folgereaktion |
1. Lineare Kennlinie
Der lineare Kennlinie Dies ist vielleicht die gebräuchlichste und am einfachsten zu verstehende Variante. Bei dieser Art von Belastung ist das Verhältnis zwischen Last und Durchbiegung direkt proportional – doppelte Kraft, doppelte Durchbiegung.
Hauptmerkmale:
- Die Kurve erscheint im Last-Verformungs-Diagramm als Gerade.
- Die Federrate (Steifigkeit) bleibt über den gesamten Arbeitsbereich konstant.
- Folgt dem Hookeschen Gesetz: F = k × f, wobei k die Federkonstante ist.
- Die meisten Schraubendruck- und -zugfedern weisen ein lineares Verhalten auf.
Wo Sie Linearfedern finden:
- Standard-Druckfedern in alltäglichen Anwendungen
- Zugfedern in Garagentoren und Trampolinen
- Torsionsfedern in Wäscheklammern und Mausefallen
- JIS- und US-Standard-Druckfedern für gleichmäßige Krafteinwirkung
Linearfedern sind die Arbeitspferde der Federnindustrie. Wenn Sie eine vorhersehbare und gleichmäßige Leistung ohne Überraschungen benötigen, sind Linearfedern in der Regel die beste Wahl.
2. Progressive (steigende) Kennlinie
A progressive oder zunehmende Charakteristikkurve Die Abbildung zeigt eine Feder, die beim Zusammendrücken oder Ausdehnen steifer wird. Die Kurve beginnt relativ flach und wird mit zunehmender Auslenkung steiler.
Mathematische Beziehung:
Bei progressiven Federn lässt sich die Beziehung wie folgt ausdrücken:
Die Änderungsrate dF/df steigt mit zunehmender Auslenkung f.
Das bedeutet, dass F'/f an jedem Punkt der Kurve größer als F/f ist.
Praktische Anwendungen:
- Fahrzeugfederungssysteme, die einen weichen Fahrkomfort bei gleichzeitig hoher Durchschlagsfestigkeit erfordern.
- Überlastschutzmechanismen
- Progressive Ventilfedern in Hochleistungsmotoren
- Konische Federn in platzbeschränkten Anwendungen
3. Degressive (fallende) Kennlinie
Das Gegenteil von progressiv, ein degressive oder abnehmende Charakteristikkurve stellt Federn dar, die beim Zusammendrücken weicher werden. Die Kurve beginnt steil und flacht dann ab.
Wo degressive Federn ihre Stärken ausspielen:
- Stoßdämpfung, wo dem ersten Aufprall entschieden entgegengewirkt werden muss
- Bestimmte Arten von Pufferanwendungen
- Spezialisierte Dämpfungssysteme
Kombinierte und komplexe Charakteristikkurven
In realen Anwendungen sind oft Federverhalten erforderlich, das sich nicht eindeutig in die drei Grundkategorien einordnen lässt. Genau hier setzt es an. kombinierte Kennlinien Hierbei kommen Federn zum Einsatz, die innerhalb ihres Arbeitsbereichs unterschiedliche Verhaltensweisen zeigen.
Kegelspiralfedern
Kegelspiralfedern Sie weisen eine der interessantesten Kombinationseigenschaften auf. Diese Federn zeigen Folgendes:
- Anfangsphase linearZu Beginn der Belastung verhält sich die Feder linear.
- ÜbergangspunktNach Erreichen einer bestimmten Auslenkung ändert sich die Charakteristik.
- Progressive PhaseDie Feder wird zunehmend steifer, wenn die Windungen ihren Anschlag erreichen.
Dieses Verhalten macht konische Federn ideal für Anwendungen, die eine kompakte Bauhöhe (die Windungen sind ineinander verschachtelt), einen kontrollierten progressiven Widerstand und eine platzsparende hohe Belastbarkeit erfordern.
Belleville (Disc) Springs
Belleville Springs Tellerfedern sind faszinierende Bauteile mit einzigartigen Kennlinien. Ihr Verhalten zeigt Folgendes:
- Anfängliche degressive PhaseDie Feder hat anfangs eine hohe Steifigkeit, die abnimmt
- Mittlerer Übergang: Eine relativ flache Region in einigen Konfigurationen
- Letzte progressive PhaseDie Steifigkeit nimmt wieder zu, wenn sich die Feder der flachen Seite annähert.
Die Gesamtkurve bildet oft eine S-Form, Dadurch sind Belleville-Federn unglaublich vielseitig einsetzbar für Anwendungen mit hoher Belastung und geringer Auslenkung, zum Spannen und Vorspannen von Schrauben, zum thermischen Ausgleich in Baugruppen und zur Energieabsorption.
Bei Cixi Dili Frühling, Wir fertigen Präzisions-Belleville-Federn nach internationalen Standards, einschließlich DIN 2093, und erfüllen damit die hohen Anforderungen unserer Kunden weltweit.
Ringfedern
Ringfedern weisen eine charakteristische Kurve mit signifikanten Hysterese—Die Be- und Entladekurven verlaufen nicht auf demselben Pfad. Das liegt daran, dass:
Bei vielen Ringfederanordnungen kann die Belastungskurve nahezu linear erscheinen, während die Entlastungskurve aufgrund von Reibungsverlusten zwischen den Ringelementen progressiver wird.
- Beim Beladen wird durch Reibung zwischen den Ringelementen Energie verbraucht.
- Die Fläche zwischen den Belastungs- und Entlastungskurven stellt die Energiedissipation dar.
- Dadurch eignen sich Ringfedern hervorragend zur Dämpfung und Schwingungsabsorption.
Kombinationsfedern
Kombinationsfedern bestehen aus zwei oder mehr zusammenwirkenden Federn, oft Federn unterschiedlicher Höhe, die parallel angeordnet sind. Ihre Charakteristik zeigt:
- Einphasen-FederphaseAnfangs trägt nur die längere Feder die Last – lineares Verhalten
- ÜbergangspunktWenn die Auslenkung den Eingriffspunkt der kürzeren Feder erreicht.
- Kombinierte PhaseBeide Federn arbeiten zusammen und erhöhen so die Gesamtgeschwindigkeit.
Federsteifigkeit und Federrate verstehen
Federsteifigkeit, auch genannt Federrate oder Federkonstante, Die Federkonstante ist ein fundamentaler Parameter, der den Widerstand einer Feder gegen Verformung quantifiziert. Sie ist definiert als das Verhältnis von Lastzunahme zu Auslenkungszunahme.

Abbildung 4: Formeln zur Berechnung der Federsteifigkeit von Druck-/Zugfedern und Drehfedern
Zusammenfassung der Steifigkeitsformeln:
Für Druck- und Zugfedern:
F' = dF/df (N/mm oder lb/in)
Für lineare Federn gilt: F' = F/f = konstant (Federrate k)
Für Torsionsfedern:
T' = dT/dφ (N·mm/Grad)
Für lineare Torsionsfedern gilt: T' = T/φ = konstant
Tangenten- vs. Sekantensteifigkeit (nichtlineare Kurven)
Bei nichtlinearen Federn hängt die “Steifigkeit” vom jeweiligen Punkt auf der Kurve ab. In Konstruktionsprüfungen und der Kommunikation mit Lieferanten werden üblicherweise zwei Werte verwendet:
- Tangentensteifigkeit (Momentansteifigkeit): die lokale Steigung an einem Arbeitspunkt, kt = dF/df
- Sekantensteifigkeit (Mittelwert): die Gerade vom Ursprung zu diesem Punkt, ks = F/f
In vielen Quellen wird die statische/Anfangsauslenkung fs wird definiert durch Erweiterung der Tangente an einem Arbeitspunkt, bis er die Auslenkungsachse schneidet. Dies ist eine praktische Methode, um eine nichtlineare Feder lokal um einen Arbeitspunkt herum zu “linearisieren”:
F ≈ kt × (f − fs)
Diese Näherung sollte nur bei kleinen Abweichungen um diesen Arbeitspunkt verwendet werden.
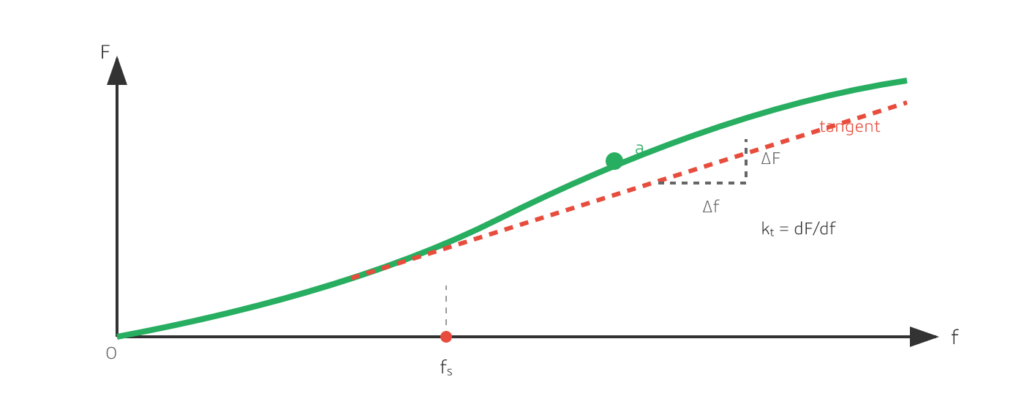
Abbildung 5: Bei einer nichtlinearen Kurve hängt die Steifigkeit vom Arbeitspunkt ab – Tangentensteifigkeit kt (dF/df) vs Sekantensteifigkeit ks (F/f), zuzüglich statischer/anfänglicher Auslenkung fs.
Verständnis der Federkonformität
Der Kehrwert der Steifigkeit wird genannt Einhaltung oder Flexibilität. Sie beschreibt die Verformung pro Einheit der aufgebrachten Kraft. Die Nachgiebigkeit ist besonders nützlich bei der Analyse von Systemen mit mehreren Federn, der Berechnung von Durchbiegungen unter bekannten Lasten und der Auslegung für spezifische Flexibilitätsanforderungen.
Wie Kennlinien die Federauswahl beeinflussen
Das Verständnis von Kennlinien ist nicht nur von akademischer Bedeutung – es hat direkten Einfluss darauf, welche Feder Sie für Ihre Anwendung wählen sollten. Lassen Sie uns untersuchen, wie verschiedene Kennlinien unterschiedlichen Zwecken dienen.
Linearfedern: Die zuverlässigen Arbeitstiere
Wenn Ihre Anwendung eine vorhersehbare Kraft in jeder Position, ein gleichbleibendes Verhalten über den gesamten Arbeitsbereich sowie eine einfache Berechnung und Spezifikation erfordert, dann sind Federn mit linearer Kennlinie die beste Wahl.
Profi-Tipp: Bei der Spezifizierung linearer Federn ist zu beachten, dass die Kraft bei jeder Auslenkung einfach F = k × f beträgt. Dies macht die Systemauslegung unkompliziert und vorhersehbar.
Progressive Federn: Sanfter Anlauf, fester Auslauf
Zu den Anwendungen, die von fortschrittlichen Eigenschaften profitieren, gehören:
Fahrzeugfederungssysteme: Moderne Fahrzeugfederungen verwenden häufig progressive Federn mit S-förmigen Kennlinien, da bei normalen Fahrbedingungen die weiche Anfangsfederung für ein komfortables Fahrgefühl aktiviert wird, bei starker Kurvenfahrt oder Unebenheiten der steifere Teil für ein kontrolliertes Fahrverhalten aktiviert wird und bei extremen Bedingungen die Federn sich der festen Federhöhe annähern, um ein Durchschlagen zu verhindern.
Hysteresekurven: Energieabsorption
Federn wie Ringfedern, die eine ausgeprägte Hysterese aufweisen, werden insbesondere dann gewählt, wenn Energie abgeführt (und nicht gespeichert und wieder freigesetzt) werden muss, eine optimale Schwingungsdämpfung entscheidend ist und eine Stoßdämpfung ohne Rückprall erforderlich ist.
Auswahl von Federn für Ihre Anwendung: Ein praktischer Rahmen
Basierend auf unserer jahrzehntelangen Erfahrung bei Cixi Dili Frühling, Hier ist ein Rahmenkonzept zur Auswahl von Federn basierend auf charakteristischen Anforderungen:
| Anwendungsart | Empfohlene Eigenschaften | Federtypen |
|---|---|---|
| Gleichmäßige Kraft über den gesamten Bereich | Linear | Druck-, Zug- und Stempelfedern |
| Sanfter Start, festes Ende | Progressiv | Konisch, variable Steigung |
| Energieabsorption | Hysterese | Ringfedern, Tellerfederpakete |
| Hohe Belastung, kleiner Platz | Variiert | Belleville, Wave Springs |
| Zweistufige Reaktion | Kombiniert | Kombinationsfedern, verschachtelt |
Checkliste für Angebotsanfragen (beschleunigt die Angebotserstellung): Teilen Sie uns den Federtyp und die Arbeitspunkte (z. B. F) mit.1 @ F1, F2 @ F2), verfügbarer Einbauraum, maximale Durchbiegung, Anforderung an die Kennlinie (linear/progressiv/degressiv), angestrebte Lebensdauer (Zyklen), Umgebungsbedingungen (Temperatur/Korrosion), Toleranzen, Material, Oberflächenbeschaffenheit und anwendbare Normen (JIS/DIN/ASTM, falls vorhanden).
Praktische Überlegungen: Von der Theorie zur Realität
Theoretische Kennlinien werden zwar mithilfe mathematischer Modelle berechnet, doch Federn in der Praxis weisen immer gewisse Abweichungen auf. Hier erfahren Sie, was Sie wissen müssen:
Fertigungstoleranzen
Selbst bei der präzisesten Fertigung – wie den Verfahren, die wir bei Cixi Dili Spring Co., Ltd.—Abweichungen entstehen aufgrund von Materialeigenschaften (Streckgrenze, Elastizitätsmodul), Maßtoleranzen (Drahtdurchmesser, Spulendurchmesser, Steigung), Wärmebehandlungsunterschieden und Oberflächenbeschaffenheit.
Brancheneinblicke: Deshalb ist es für kritische Anwendungen unerlässlich, reale Federmuster zu testen. Bei Dili Spring fertigen wir Federn nach Kundenvorgaben oder Zeichnungen und überprüfen anschließend die Leistungsfähigkeit durch Belastungstests, um sicherzustellen, dass die Kennlinien den Spezifikationen entsprechen.
Temperatureinflüsse
Die Temperatur beeinflusst das Verhalten von Federn maßgeblich: Höhere Temperaturen verringern im Allgemeinen die Steifigkeit, die Wärmeausdehnung verändert die Federgeometrie, und die Materialeigenschaften (insbesondere der Elastizitätsmodul) variieren mit der Temperatur. Für Hochtemperaturanwendungen ist die richtige Materialauswahl (z. B. Federstahldraht für moderate Temperaturen oder Inconel für extreme Hitze) unerlässlich.
Warum mit einem erfahrenen Federnhersteller zusammenarbeiten?
Die Komplexität von Federkennlinien und Steifigkeitsberechnungen unterstreicht die Bedeutung der Zusammenarbeit mit kompetenten Herstellern. Hier ist, was Cixi Dili Spring Co., Ltd. bringt Folgendes ein:
Lokaler Support + weltweiter Versand: Mit Sitz in Cixi (Ningbo), Zhejiang, China, unterstützen wir OEMs weltweit mit schneller Mustererstellung und exportfertiger Dokumentation.
Drei Jahrzehnte Erfahrung: Seit 1995 fertigen wir Federn für Kunden weltweit und verfügen über umfassende Expertise in den Bereichen JIS-Standard-Druckfedern, US-Standard-Druckfedern, Torsionsfedern, Druckfedern, Federn aus Federstahldraht, Zugfedern und kundenspezifisch geformte Federn für besondere Anwendungen.
Vollständige Leistungsfähigkeit: Unser integriertes Forschungs-, Entwicklungs-, Produktions- und Vertriebssystem ermöglicht es uns, die technischen Aspekte Ihrer Anforderungen zu verstehen, optimale Lösungen auf Basis der benötigten Kennlinien vorzuschlagen und eine strenge Qualitätskontrolle nach internationalen Standards aufrechtzuerhalten.
Exzellente Individualisierung: Jede Anwendung ist einzigartig. Wir freuen uns über kundenspezifische Designs nach Ihren Zeichnungen, Reverse Engineering anhand Ihrer Muster und die gemeinsame Entwicklung neuer Anwendungen.
Abschluss
Federkennlinien und Federsteifigkeiten sind grundlegende Konzepte, die erfolgreiche von problematischen technischen Anwendungen unterscheiden. Durch das Verständnis der drei grundlegenden Kurventypen – linear, progressiv und degressiv – und ihrer Kombinationen erlangen Sie die Fähigkeit:
- Genau vorhersagen Spring-Verhalten in Ihren Anwendungen
- Optimale Federn auswählen die genau Ihren Anforderungen entsprechen
- Fehlerbehebung bei Problemen wenn Federn nicht wie erwartet funktionieren
- Effektiv kommunizieren mit Federlieferanten über Ihre Bedürfnisse
Denken Sie daran: Die Kennlinie beschreibt das gesamte Verhalten einer Feder. Ob Sie die zuverlässige Gleichmäßigkeit einer linearen Druckfeder, das fein abgestimmte Ansprechverhalten einer progressiven Automobilfeder oder die energieabsorbierenden Eigenschaften eines Ringfedersystems benötigen – das Verständnis dieser Kennlinien ist der Schlüssel zum Erfolg.
Häufig gestellte Fragen (FAQs)
1. Worin besteht der Unterschied zwischen Federrate und Federsteifigkeit?
Federrate Und Federsteifigkeit Die Begriffe beschreiben im Wesentlichen dasselbe Konzept: die Kraft, die benötigt wird, um eine Feder um eine Einheitsstrecke auszulenken (typischerweise in N/mm oder lb/in angegeben). Bei linearen Federn ist dies ein konstanter Wert. Bei nichtlinearen Federn variiert die Federrate mit der Auslenkung, daher wird üblicherweise die momentane Federrate an einem bestimmten Auslenkungspunkt angegeben. Die Begriffe werden in der Praxis synonym verwendet.
2. Kann eine einzelne Feder mehrere charakteristische Kurvenverläufe aufweisen?
Ja, absolut! Kombinierte Kennlinien Sie sind weit verbreitet. Eine Druckfeder mit variabler Steigung beispielsweise beginnt mit weicheren Windungen, die sich zuerst schließen (lineares Verhalten), und geht dann in steifere Windungen über (progressives Verhalten). Tellerfederpakete lassen sich so konstruieren, dass sie nahezu jede gewünschte Eigenschaft aufweisen, indem die Anordnung und Anzahl der Federn in Reihe und parallel variiert wird.
3. Wie messe ich die Kennlinie einer vorhandenen Feder?
Um die Kennlinie einer Feder zu ermitteln, benötigen Sie eine Prüfvorrichtung: Montieren Sie die Feder in einer Prüfvorrichtung, erhöhen Sie die Last schrittweise, erfassen Sie die Durchbiegung bei jedem Lastpunkt, tragen Sie die Datenpunkte in ein Diagramm ein und verbinden Sie diese, um die Kennlinie zu erhalten. Für präzise Messungen können automatisierte Federprüfmaschinen diese Kennlinien schnell und genau erzeugen.
4. Warum zeigen manche Federn beim Belasten und Entlasten unterschiedliche Kurvenverläufe?
Dieses Phänomen wird genannt Hysterese Sie entsteht durch Energieverluste während des Betriebs der Feder. Zu den Ursachen zählen Reibung zwischen den Windungen oder Federelementen (insbesondere bei Ringfedern und Tellerfederpaketen), interne Materialdämpfung (besonders ausgeprägt bei Gummi- oder Polymerfedern) und mechanische Interferenzen in bestimmten Federkonstruktionen. Die Fläche zwischen Belastungs- und Entlastungskurve entspricht der als Wärme dissipierten Energie.
5. Wie wirkt sich die Temperatur auf die Federkennlinie aus?
Die Temperatur beeinflusst Federn auf verschiedene Weise: Der Elastizitätsmodul des Materials sinkt bei höheren Temperaturen (wodurch die Steifigkeit abnimmt), die Streckgrenze ändert sich (was die maximale Belastbarkeit beeinflusst), die Wärmeausdehnung verändert die Federgeometrie, und die Spannungsrelaxation beschleunigt sich bei erhöhten Temperaturen. Für Hochtemperaturanwendungen ist die Materialwahl entscheidend. Standard-Kohlenstoffstahlfedern können bei erhöhten Temperaturen 10–151 TP13T ihrer Federrate verlieren, während Speziallegierungen wie Inconel ihre Eigenschaften deutlich besser beibehalten.
6. Worin besteht der Unterschied zwischen Sekantensteifigkeit (F/f) und Tangentensteifigkeit (dF/df)?
Auf einer nichtlinearen Kennlinie, Sekantensteifigkeit F/f ist die durchschnittliche Änderungsrate vom Ursprung zu einem Punkt, während Tangentensteifigkeit dF/df ist die momentane Steigung am Arbeitspunkt. Verwenden Sie die Tangentensteifigkeit zur Analyse kleiner Variationen um einen Arbeitspunkt und die Sekantensteifigkeit für schnelle Abschätzungen über den gesamten Bereich.
Über Cixi Dili Spring Co., Ltd.
Cixi Dili Spring Co., Ltd. ist seit 1995 ein vertrauenswürdiger Name in der Federnherstellung. Wir sind spezialisiert auf die Produktion hochwertiger Federn für Kunden weltweit, darunter Druckfedern (JIS- und US-Standard), Torsionsfedern, Druckfedern, Zugfedern, Federn aus Federstahldraht und Federn in Sonderformen.
Unser integrierter Ansatz – der Forschung und Entwicklung, Produktion und Vertrieb umfasst – gewährleistet, dass jede von uns gelieferte Frühjahrskollektion internationalen Standards und kundenspezifischen Anforderungen entspricht.
Nehmen Sie noch heute Kontakt mit uns auf:
E-Mail: [email protected]
WhatsApp: +86 13586942004