Guía completa sobre curvas características y rigidez de resortes

¿Alguna vez te has preguntado por qué algunos resortes se sienten más rígidos al comprimirlos, mientras que otros mantienen una resistencia constante durante todo su recorrido? ¿O por qué ciertas aplicaciones industriales requieren resortes con comportamientos de carga-deflexión muy específicos? La respuesta está en comprender curvas características del resorte y rigidez—dos conceptos fundamentales que todo ingeniero, diseñador y especialista en adquisiciones debe dominar.

En esta guía completa, profundizaremos en la ciencia detrás de las curvas características de los resortes, exploraremos los diferentes tipos de curvas y sus implicaciones prácticas, y le ayudaremos a seleccionar el resorte adecuado para su aplicación específica. Ya sea que diseñe sistemas de moldes, suspensiones automotrices o dispositivos electrónicos de precisión, este conocimiento le resultará invaluable.

Respuesta rápida (60 segundos)

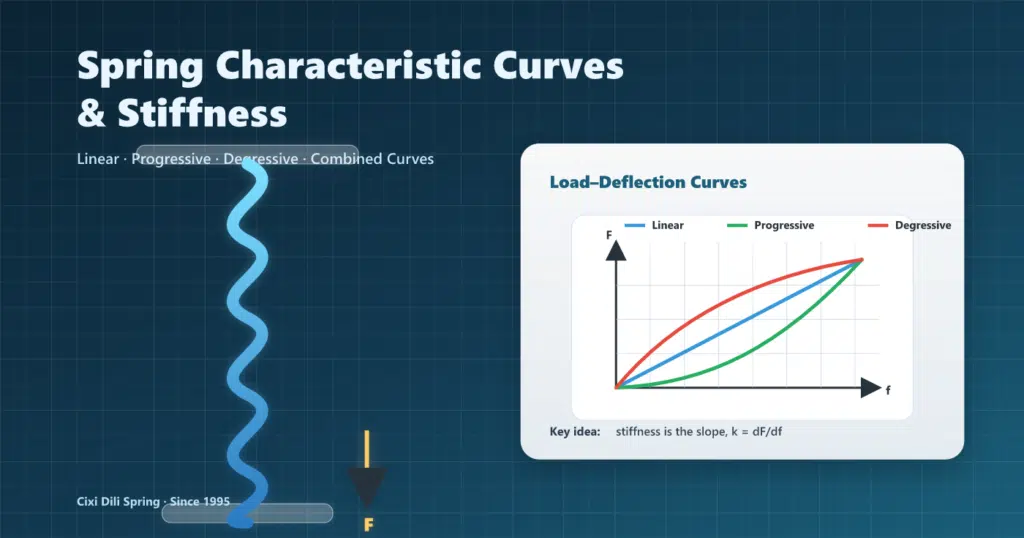
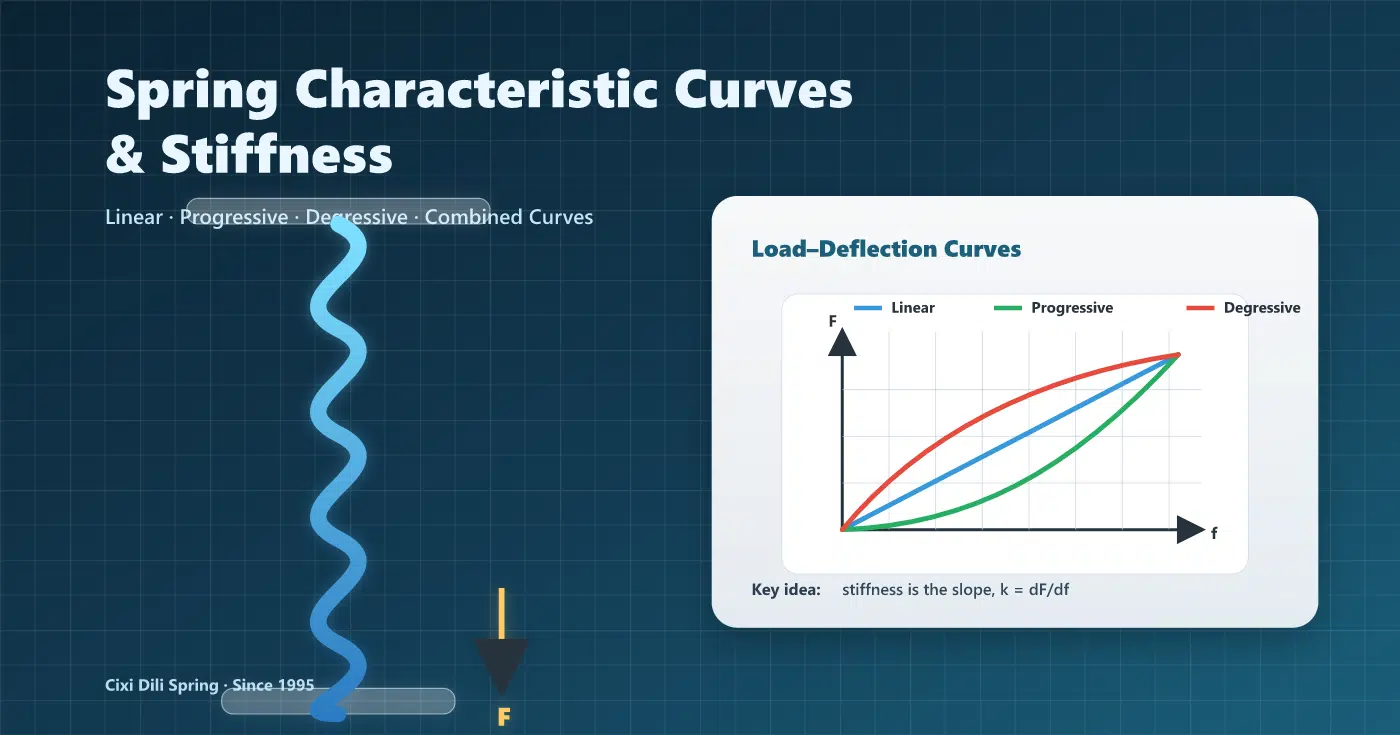
• Curva característica del resorte = la relación fuerza-deflexión (F–f) o par-ángulo (T–φ).
• Rigidez / tasa de resorte en un punto la pendiente de la curva es: k = dF/df (o k_θ = dT/dφ).
• Lineal: k constante. Progresivo:k aumenta con la desviación. Decreciente:k disminuye con la desviación.
• En curvas no lineales, distinguir rigidez tangente (dF/df) frente a rigidez secante (F/f) en el punto de trabajo.

Tabla de contenido

• ¿Qué son las curvas características del resorte?
• Tres tipos de curvas fundamentales
• Curvas combinadas y complejas
• Rigidez del resorte y tasa de resorte
• Cómo las curvas guían la selección
• Un marco de selección práctico
• Consideraciones prácticas
• ¿Por qué asociarse con un fabricante?
• Conclusión
• Preguntas frecuentes

¿Qué son las curvas características del resorte?

A curva característica del resorte representa la relación entre la carga (fuerza F o par T) aplicada a un resorte y la deformación resultante (deflexión f o desplazamiento angular φ). En pocas palabras, es una representación gráfica de cómo un resorte responde al aumento de cargas.

Piénsalo así: si presionas un resorte con la mano y mides tanto la fuerza aplicada como la compresión del resorte, y luego representas esos valores en un gráfico, crearás una curva característica. Esta curva describe el comportamiento completo de ese resorte bajo carga.

¿Por qué son importantes las curvas características?

Comprender las curvas características es crucial por varias razones:

• Rendimiento predecible:Los ingenieros pueden predecir con precisión cómo funcionará un resorte en una aplicación determinada.
• Gestión de carga:Conocer la curva ayuda a diseñar sistemas que gestionen las cargas de manera eficaz.
• Consideraciones de seguridad:Las aplicaciones críticas requieren un conocimiento preciso del comportamiento del resorte en condiciones extremas.
• Optimización de costos:Seleccionar el tipo de resorte correcto reduce la ingeniería excesiva y los costos innecesarios.

En Cixi Dili Spring Co., Ltd., Fabricamos resortes desde 1995 y podemos decirle por experiencia que comprender estas curvas es a menudo la diferencia entre una aplicación exitosa y un fracaso costoso.

Los tres tipos fundamentales de curvas características de resorte

Las curvas características de los resortes se pueden clasificar en tres tipos fundamentales, cada uno con comportamientos y aplicaciones distintos.

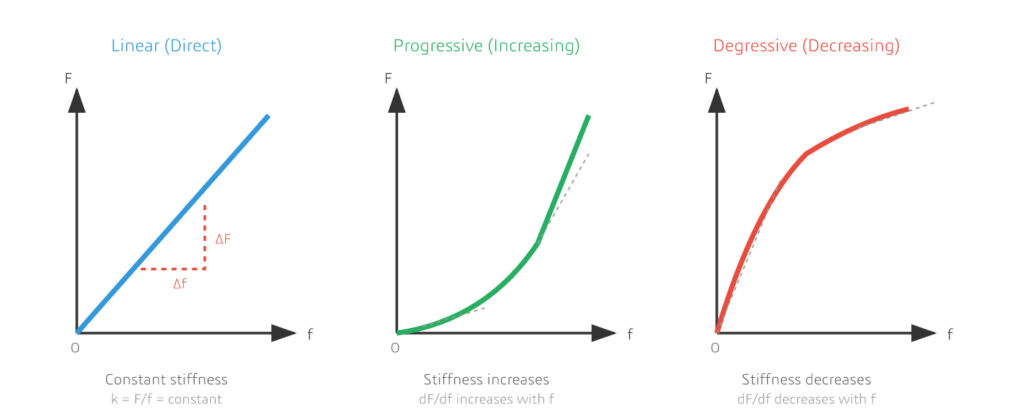
Figura 2: Los tres tipos fundamentales de curvas características de resorte: lineal, progresiva (creciente) y degresiva (decreciente)

Tipo de curva	¿Qué sucede con la rigidez (k)?	Diseños típicos	Mejor para
Lineal	Constante: k = dF/df es el mismo en todo el rango de trabajo	La mayoría de los resortes helicoidales de compresión/extensión, resortes de matriz estándar	Fuerza predecible en cualquier posición, fácil dimensionamiento y control.
Progresivo	Creciente: k crece a medida que aumenta la desviación	Paso variable, resortes cónicos, diseños que ponen en contacto las bobinas	Respuesta inicial suave, resistencia a sobrecargas/toques de fondo
Decreciente	Disminuyendo: k disminuye a medida que aumenta la desviación	Geometrías/sistemas de materiales especiales; algunas pilas de resortes	Alta resistencia inicial con respuesta de seguimiento más suave

1. Curva característica lineal

El curva característica lineal Es quizás el más común y fácil de entender. En este tipo, la relación entre carga y deflexión es directamente proporcional: al doble de fuerza, doble deflexión.

Características principales:

• La curva aparece como una línea recta en un gráfico de carga-deflexión.
• La tasa de resorte (rigidez) permanece constante en todo el rango de trabajo.
• Sigue la ley de Hooke: F = k × f, donde k es la constante del resorte
• La mayoría de los resortes helicoidales de compresión y extensión exhiben un comportamiento lineal.

Dónde encontrará resortes lineales:

• Resortes de compresión estándar en aplicaciones cotidianas
• Resortes de extensión en puertas de garaje y trampolines
• Resortes de torsión en pinzas de ropa y trampas para ratones
• Resortes de matriz estándar JIS y de EE. UU. para una aplicación de fuerza constante

Los resortes lineales son los caballos de batalla de la industria. Cuando se necesita un rendimiento predecible y constante sin sorpresas, los resortes lineales característicos suelen ser la mejor opción.

2. Curva característica progresiva (creciente)

A curva característica progresiva o creciente Muestra un resorte que se vuelve más rígido al comprimirse o extenderse. La curva comienza relativamente plana y se vuelve más pronunciada a medida que aumenta la deflexión.

Relación matemática:

Para resortes progresivos, la relación se puede expresar como:

La tasa de cambio dF/df aumenta a medida que aumenta la deflexión f

Esto significa que F'/f > F/f en cualquier punto de la curva.

Aplicaciones prácticas:

• Sistemas de suspensión automotriz que requieren una conducción suave con una resistencia firme al tocar fondo
• Mecanismos de protección contra sobrecargas
• Resortes de válvulas de velocidad progresiva en motores de alto rendimiento
• Resortes cónicos en aplicaciones con limitaciones de espacio

3. Curva característica decreciente

Lo opuesto de progresista, un curva característica decreciente o decreciente Representa resortes que se ablandan al comprimirse. La curva empieza pronunciada y se aplana.

Dónde sobresalen los manantiales degresivos:

• Absorción de impactos donde el impacto inicial necesita ser firmemente resistido
• Ciertos tipos de aplicaciones de buffer
• Sistemas de amortiguación especializados

Curvas características combinadas y complejas

Las aplicaciones del mundo real a menudo requieren comportamientos de resortes que no encajan perfectamente en las tres categorías básicas. Aquí es donde curvas características combinadas entran en juego: resortes que exhiben múltiples comportamientos a lo largo de su rango de trabajo.

Resortes de voluta cónica

Muelles de voluta cónica Presentan una de las características combinadas más interesantes. Estos manantiales presentan:

• Fase lineal inicial:Al inicio de la carga, el resorte se comporta linealmente.
• Punto de transición:Después de alcanzar una cierta desviación, la característica cambia
• Fase progresiva:El resorte se vuelve cada vez más rígido a medida que las bobinas comienzan a tocar fondo.

Este comportamiento hace que los resortes cónicos sean ideales para aplicaciones que requieren una altura sólida compacta (las bobinas se anidan una dentro de la otra), una resistencia progresiva controlada y una capacidad de carga alta que ahorra espacio.

Resortes Belleville (disco)

Manantiales de Belleville Los resortes de disco son componentes fascinantes con curvas características únicas. Su comportamiento muestra:

• Fase degresiva inicial:El resorte comienza con una rigidez alta que disminuye
• Transición media:Una región relativamente plana en algunas configuraciones
• Fase progresiva final:La rigidez aumenta nuevamente a medida que el resorte se acerca al plano.

La curva general a menudo forma una forma de S, lo que hace que los resortes Belleville sean increíblemente versátiles para aplicaciones de alta carga y pequeña deflexión, tensado y precarga de pernos, compensación térmica en conjuntos y absorción de energía.

En Cixi Dili Primavera, Fabricamos resortes Belleville de precisión según estándares internacionales, incluido DIN 2093, satisfaciendo así los exigentes requisitos de clientes de todo el mundo.

Resortes de anillo

Muelles de anillo presentan una curva característica con valores significativos histéresis—Las curvas de carga y descarga no siguen la misma trayectoria. Esto se debe a que:

En muchos conjuntos de resortes de anillo, la curva de carga puede parecer casi lineal, mientras que la curva de descarga se vuelve más progresiva debido a las pérdidas por fricción entre los elementos del anillo.

• Durante la carga, la fricción entre los elementos del anillo consume energía.
• El área entre las curvas de carga y descarga representa la disipación de energía.
• Esto hace que los resortes de anillo sean excelentes para la amortiguación y la absorción de vibraciones.

Resortes combinados

Muelles combinados Consisten en dos o más resortes que trabajan juntos, a menudo resortes de diferentes alturas dispuestos en paralelo. Sus características son:

• Fase de resorte único: Inicialmente, solo el resorte más alto soporta la carga: comportamiento lineal
• Punto de transición:Cuando la desviación alcanza el punto de enganche del resorte más corto
• Fase combinada:Ambos resortes trabajan juntos, aumentando la tasa general.

Comprensión de la rigidez y la tasa de resorte

Rigidez del resorte, también llamado tasa de resorte o constante de resorte, Es un parámetro fundamental que cuantifica la resistencia de un resorte a la deformación. Se define como la relación entre el incremento de carga y el incremento de deflexión.

Figura 4: Fórmulas de rigidez de resortes para resortes de compresión/extensión y resortes de torsión

Resumen de fórmulas de rigidez:

Para resortes de compresión y extensión:

F' = dF/df (N/mm o lb/pulg.)

Para resortes lineales: F' = F/f = constante (tasa de resorte k)

Para resortes de torsión:

T' = dT/dφ (N·mm/grado)

Para resortes de torsión lineales: T' = T/φ = constante

Rigidez tangente vs. secante (curvas no lineales)

Para resortes no lineales, la rigidez depende de su posición en la curva. Se utilizan comúnmente dos valores en las revisiones de diseño y la comunicación con los proveedores:

• Rigidez tangente (instantánea):la pendiente local en un punto de trabajo, k_t = dF/df
• Rigidez secante (promedio):la línea desde el origen hasta ese punto, k_s = F/f

En muchas referencias, el deflexión estática/inicial f_s se define extendiendo el tangente En un punto de trabajo hasta que interseca el eje de deflexión. Esta es una forma práctica de linealizar localmente un resorte no lineal alrededor de un punto de trabajo:

F ≈ k_t × (f − f_s)

Utilice esta aproximación sólo para pequeñas variaciones alrededor de ese punto de trabajo.

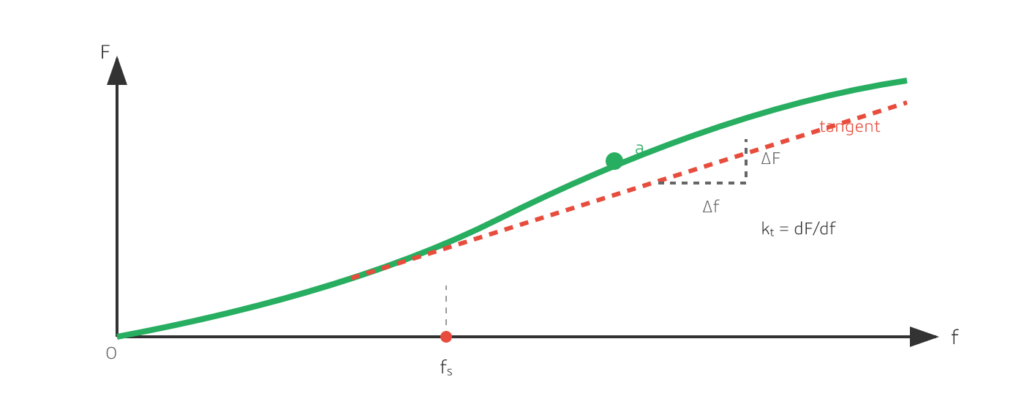
Figura 5: En una curva no lineal, la rigidez depende del punto de trabajo: rigidez tangente k_t (dF/df) vs rigidez secante k_s (F/f), más la deflexión estática/inicial f_s.

Comprensión del cumplimiento de Spring

El inversa de la rigidez se llama cumplimiento o flexibilidad. Representa la deformación producida por unidad de fuerza aplicada. La flexibilidad es especialmente útil al analizar sistemas con múltiples resortes, calcular deflexiones a partir de cargas conocidas y diseñar para requisitos específicos de flexibilidad.

Cómo las curvas características guían la selección de resortes

Comprender las curvas características no es solo una cuestión académica: influye directamente en el resorte que debe elegir para su aplicación. Exploremos cómo las diferentes curvas cumplen distintas funciones.

Resortes lineales: los caballos de batalla confiables

Si su aplicación requiere una fuerza predecible en cualquier posición, un comportamiento consistente en todo el rango de trabajo y un cálculo y especificación sencillos, entonces los resortes característicos lineales son su mejor opción.

Consejo profesional: Al especificar resortes lineales, recuerde que la fuerza en cualquier deflexión es simplemente F = k × f. Esto hace que el diseño del sistema sea sencillo y predecible.

Resortes progresivos: arranque suave, acabado firme

Las aplicaciones que se benefician de las características progresivas incluyen:

Sistemas de suspensión de vehículos: Las suspensiones de los automóviles modernos a menudo utilizan resortes progresivos con curvas en forma de S porque las condiciones normales de conducción activan la tasa inicial suave para un andar cómodo, las curvas difíciles o los baches activan la parte más rígida para un manejo controlado y las condiciones extremas se aproximan a la altura sólida para la protección contra el toque de fondo.

Curvas de histéresis: absorción de energía

Los resortes como los resortes de anillo que muestran una histéresis significativa se eligen específicamente cuando se debe disipar energía (no almacenarla y liberarla), la amortiguación de vibraciones es fundamental y se requiere absorción de impacto sin rebote.

Selección de resortes para su aplicación: un marco práctico

Basándonos en nuestras décadas de experiencia en Cixi Dili Primavera, A continuación se presenta un marco para seleccionar resortes según requisitos característicos:

Tipo de aplicación	Característica recomendada	Tipos de resortes
Fuerza constante en todo el rango	Lineal	Resortes de compresión, extensión y matriz
Inicio suave, final firme	Progresivo	Cónico, paso variable
Absorción de energía	Histéresis	Muelles de anillo, pilas de muelles de disco
Alta carga, espacio pequeño	Varía	Belleville, Wave Springs
Respuesta en dos etapas	Conjunto	Resortes combinados, anidados

Lista de verificación de RFQ (acelera la cotización): Compartir el tipo de resorte, puntos de trabajo (por ejemplo, F₁ @f₁, F₂ @f₂), espacio de instalación disponible, deflexión máxima, requisito de velocidad/curva (lineal/progresiva/degresiva), objetivo de vida (ciclos), entorno (temperatura/corrosión), tolerancias, material, acabado de superficie y estándares aplicables (JIS/DIN/ASTM si los hay).

Consideraciones prácticas: de la teoría a la realidad

Si bien las curvas características teóricas se calculan mediante modelos matemáticos, los resortes reales siempre presentan cierta desviación. Esto es lo que necesita saber:

Tolerancias de fabricación

Incluso con los procesos de fabricación más precisos, como los que utilizamos en Cixi Dili Spring Co., Ltd.—Las variaciones ocurren debido a variaciones en las propiedades del material (límite elástico, módulo), tolerancias dimensionales (diámetro del alambre, diámetro de la bobina, paso), variaciones en el tratamiento térmico y efectos del acabado de la superficie.

Perspectiva de la industria: Por eso, las aplicaciones críticas siempre requieren pruebas de resortes reales. En Dili Spring, fabricamos resortes según muestras o planos del cliente y verificamos su rendimiento mediante pruebas de carga para garantizar que las curvas características cumplan con las especificaciones.

Efectos de la temperatura

La temperatura afecta significativamente el comportamiento del resorte: las temperaturas más altas generalmente reducen la rigidez, la expansión térmica altera la geometría del resorte y las propiedades del material (especialmente el módulo) varían con la temperatura. Para aplicaciones de alta temperatura, es fundamental seleccionar el material adecuado (como el alambre de piano para temperaturas moderadas o el Inconel para temperaturas extremas).

¿Por qué asociarse con un fabricante de resortes experimentado?

La complejidad de las curvas características de los resortes y los cálculos de rigidez subrayan la importancia de trabajar con fabricantes expertos. A continuación, se detalla lo siguiente: Cixi Dili Spring Co., Ltd. trae a la mesa:

Soporte local + envío global: Con sede en Cixi (Ningbo), Zhejiang, China, apoyamos a fabricantes de equipos originales (OEM) de todo el mundo con muestreo rápido y documentación lista para exportar.

Tres décadas de experiencia: Desde 1995, hemos estado fabricando resortes para clientes globales, desarrollando una profunda experiencia en resortes de matriz estándar JIS, resortes de matriz estándar de EE. UU., resortes de torsión, resortes de compresión, resortes de alambre de música, resortes de extensión y resortes de forma personalizada para aplicaciones únicas.

Capacidades completas: Nuestro sistema integrado de I+D, producción y ventas significa que entendemos la ingeniería detrás de sus requisitos, podemos sugerir soluciones óptimas en función de las necesidades de la curva característica y mantenemos un estricto control de calidad según los estándares internacionales.

Excelencia en personalización: Cada aplicación es única. Aceptamos diseños personalizados a partir de sus planos, ingeniería inversa a partir de sus muestras y desarrollo colaborativo para nuevas aplicaciones.

Conclusión

Las curvas características de los resortes y la rigidez son conceptos fundamentales que distinguen las aplicaciones de ingeniería exitosas de las problemáticas. Al comprender los tres tipos básicos de curvas (lineales, progresivas y degresivas) y sus combinaciones, podrá:

1. Predecir con precisión Comportamiento del resorte en sus aplicaciones
2. Seleccionar resortes óptimos que coincidan exactamente con sus requisitos
3. Solucionar problemas Cuando los resortes no funcionan como se esperaba
4. Comunicarse eficazmente Con proveedores de resortes sobre sus necesidades

Recuerde, la curva característica describe el comportamiento completo de un resorte. Ya sea que necesite la consistencia confiable de un resorte de matriz lineal, la respuesta sofisticada de un resorte automotriz progresivo o las propiedades de absorción de energía de un sistema de resorte de anillo, comprender estas curvas es la clave del éxito.

Preguntas frecuentes (FAQ)

1. ¿Cuál es la diferencia entre la tasa de resorte y la rigidez del resorte?

Tasa de resorte y rigidez del resorte Son esencialmente el mismo concepto: ambos describen la fuerza necesaria para desviar un resorte una unidad de distancia (normalmente expresada en N/mm o lb/in). Para resortes lineales, este es un valor constante. Para resortes no lineales, la "velocidad" varía con la deflexión, por lo que normalmente nos referimos a la velocidad instantánea en un punto de deflexión específico. Los términos se utilizan indistintamente en la industria.

2. ¿Puede un solo resorte tener múltiples comportamientos de curvas características?

¡Sí, por supuesto! Curvas características combinadas Son bastante comunes. Un resorte de compresión de paso variable, por ejemplo, comienza con espiras más blandas que se cierran primero (comportamiento lineal) y luego pasa a espiras más rígidas (comportamiento progresivo). Los conjuntos de resortes de disco pueden diseñarse para exhibir casi cualquier característica deseada variando la disposición y el número de resortes en serie y en paralelo.

3. ¿Cómo mido la curva característica de un resorte existente?

Para medir la curva característica de un resorte, necesitará un equipo de prueba de carga: monte el resorte en un dispositivo de prueba, aplique cargas incrementales, registre la deflexión en cada punto de carga, trace los puntos de datos de carga-deflexión y conecte los puntos para obtener la curva característica. Para trabajos de precisión, las máquinas automatizadas de prueba de resortes pueden generar estas curvas con rapidez y precisión.

4. ¿Por qué algunos resortes muestran curvas diferentes durante la carga y la descarga?

Este fenómeno se llama histéresis y se produce debido a pérdidas de energía durante el funcionamiento del resorte. Las causas incluyen la fricción entre espiras o elementos del resorte (especialmente en resortes de anillo y conjuntos de resortes de disco), la amortiguación interna del material (más significativa en resortes de caucho o polímero) y la interferencia mecánica en ciertos diseños de resortes. El área entre las curvas de carga y descarga representa la energía disipada en forma de calor.

5. ¿Cómo afecta la temperatura a las curvas características del resorte?

La temperatura afecta a los resortes de diversas maneras: el módulo del material disminuye a temperaturas más altas (reduciendo la rigidez), el límite elástico cambia (lo que afecta la capacidad de carga máxima), la expansión térmica altera la geometría del resorte y la relajación de la tensión se acelera a temperaturas elevadas. Para aplicaciones de alta temperatura, la selección del material es crucial. Los resortes estándar de acero al carbono pueden perder entre un 10% y un 15% de su índice de fluencia a temperaturas elevadas, mientras que las aleaciones especiales como el Inconel mantienen sus propiedades mucho mejor.

6. ¿Cuál es la diferencia entre la rigidez secante (F/f) y la rigidez tangente (dF/df)?

En una curva característica no lineal, rigidez secante F/f es la tasa promedio desde el origen hasta un punto, mientras que rigidez tangente dF/df es la pendiente instantánea en el punto de trabajo. Utilice la rigidez tangente para analizar pequeñas variaciones alrededor de un punto de trabajo y la rigidez secante para obtener estimaciones rápidas en todo el rango.

Acerca de Cixi Dili Spring Co., Ltd.

Cixi Dili Spring Co., Ltd. ha sido un nombre confiable en la fabricación de resortes desde 1995. Nos especializamos en producir resortes de alta calidad para clientes globales, incluidos resortes de matriz (estándar JIS y estadounidense), resortes de torsión, resortes de compresión, resortes de extensión, resortes de alambre musical y resortes con formas personalizadas.

Nuestro enfoque integrado, que abarca I+D, producción y ventas, garantiza que cada resorte que entregamos cumpla con los estándares internacionales y los requisitos específicos de los clientes.

Contáctenos hoy:
Correo electrónico: [email protected]
WhatsApp: +86 13586942004

• Facebook
• YouTube
• TikTok