Você já se perguntou por que algumas molas parecem mais rígidas ao serem comprimidas, enquanto outras mantêm uma resistência constante ao longo de todo o seu curso? Ou por que certas aplicações industriais exigem molas com comportamentos de carga-deflexão muito específicos? A resposta está na compreensão. curvas características da mola e rigidez—dois conceitos fundamentais que todo engenheiro, projetista e especialista em compras deve dominar.
Neste guia completo, vamos explorar a fundo a ciência por trás das curvas características das molas, analisar os diferentes tipos de curvas e suas implicações práticas, e ajudar você a entender como selecionar a mola certa para sua aplicação específica. Seja você um projetista de sistemas de moldes, suspensões automotivas ou dispositivos eletrônicos de precisão, esse conhecimento será inestimável.
Resposta rápida (60 segundos)
- Curva característica da mola = a relação força-deflexão (F-f) ou torque-ângulo (T-φ).
- Rigidez / taxa de mola em um ponto é a inclinação da curva: k = dF/df (ou kθ = dT/dφ).
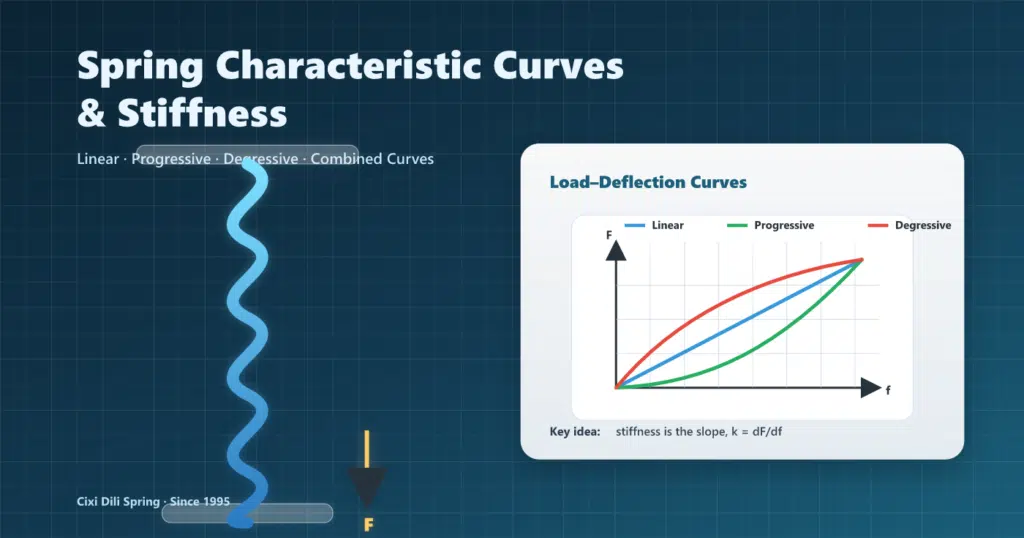
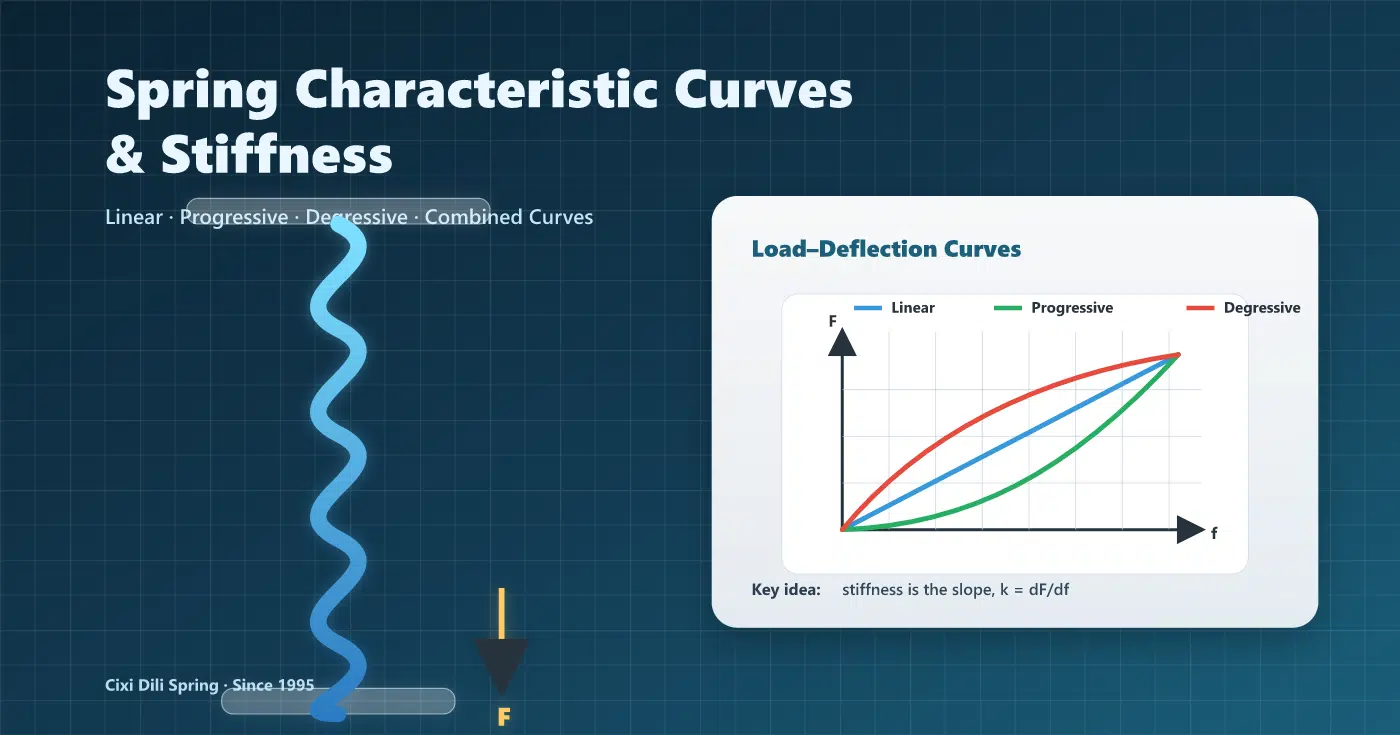
- Linear: k constante. Progressivo: k aumenta com a deflexão. DegressivoO valor de k diminui com a deflexão.
- Em curvas não lineares, distinguir rigidez tangente (dF/df) vs rigidez secante (F/f) no ponto de trabalho.
Índice
- O que são curvas características de molas?
- Três tipos fundamentais de curvas
- Curvas Combinadas e Complexas
- Rigidez e taxa de mola
- Como as curvas guiam a seleção
- Um Quadro de Seleção Prático
- Considerações práticas
- Por que fazer parceria com um fabricante?
- Conclusão
- Perguntas frequentes
O que são curvas características de molas?
A curva característica da mola representa a relação entre a carga (força) F ou torque T) aplicada a uma mola e a deformação resultante (deflexão) f ou deslocamento angular φEm termos simples, é uma representação gráfica de como uma mola responde ao aumento da carga.
Imagine o seguinte: se você pressionar uma mola com a mão e medir a força aplicada e a compressão da mola, e depois plotar esses valores em um gráfico, você criará uma curva característica. Essa curva descreve completamente o comportamento daquela mola específica sob carga.
Por que as curvas características são importantes?
Compreender as curvas características é crucial por vários motivos:
- Desempenho previsívelOs engenheiros conseguem prever com precisão o desempenho de uma mola em uma determinada aplicação.
- Gerenciamento de cargaConhecer a curva ajuda a projetar sistemas que gerenciem cargas de forma eficaz.
- Considerações de segurançaAplicações críticas exigem conhecimento preciso do comportamento de molas sob condições extremas.
- Otimização de custosSelecionar o tipo certo de mola reduz o excesso de projeto e os custos desnecessários.
No Cixi Dili Spring Co., Ltd., Fabricamos molas desde 1995 e, por experiência própria, podemos afirmar que compreender essas curvas costuma ser a diferença entre uma aplicação bem-sucedida e uma falha dispendiosa.
Os três tipos fundamentais de curvas características de molas
As curvas características das molas podem ser amplamente categorizadas em três tipos fundamentais, cada um com comportamentos e aplicações distintos.
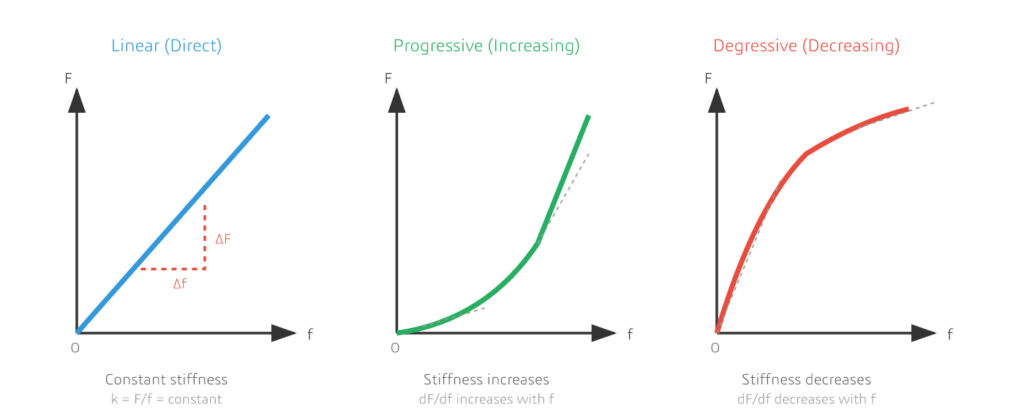
Figura 2: Os três tipos fundamentais de curvas características de molas – Linear, Progressiva (Crescente) e Degressiva (Decrescente)
| Tipo de curva | O que acontece com a rigidez (k) | Desenhos típicos | Ideal para |
|---|---|---|---|
| Linear | Constante: k = dF/df é a mesma em toda a faixa de operação. | A maioria das molas helicoidais de compressão/extensão, molas de matriz padrão | Força previsível em qualquer posição, dimensionamento e controle fáceis. |
| Progressivo | Crescente: k aumenta à medida que a deflexão aumenta. | Molas cônicas de passo variável, com designs que colocam as espiras em contato. | Resposta inicial suave, resistência à sobrecarga/impacto no fundo |
| Degressivo | Diminuindo: k diminui à medida que a deflexão aumenta. | Geometrias/sistemas de materiais especiais; algumas pilhas de molas | Alta resistência inicial com resposta subsequente mais fraca |
1. Curva Característica Linear
O curva característica linear É talvez o tipo mais comum e fácil de entender. Nesse tipo, a relação entre carga e deflexão é diretamente proporcional — o dobro da força, o dobro da deflexão.
Principais características:
- A curva aparece como uma linha reta em um gráfico de carga-deflexão.
- A constante elástica (rigidez) da mola permanece constante em toda a faixa de trabalho.
- Segue a Lei de Hooke: F = k × f, onde k é a constante elástica da mola.
- A maioria das molas helicoidais de compressão e extensão apresenta comportamento linear.
Onde você encontrará molas lineares:
- Molas de compressão padrão em aplicações do dia a dia
- Molas de extensão em portas de garagem e trampolins
- Molas de torção em prendedores de roupa e ratoeiras
- Molas de matriz padrão JIS e EUA para aplicação de força consistente
As molas lineares são os pilares da indústria de molas. Quando você precisa de um desempenho previsível e consistente, sem surpresas, as molas de característica linear são geralmente a melhor escolha.
2. Curva Característica Progressiva (Crescente)
A curva característica progressiva ou crescente A figura mostra uma mola que se torna mais rígida à medida que é comprimida ou estendida. A curva começa relativamente plana e torna-se mais íngreme conforme a deflexão aumenta.
Relação matemática:
Para molas progressivas, a relação pode ser expressa como:
A taxa de variação dF/df aumenta à medida que a deflexão f aumenta.
Isso significa que F'/f > F/f em qualquer ponto da curva.
Aplicações práticas:
- Sistemas de suspensão automotiva que exigem uma condução macia com firme resistência ao impacto final
- Mecanismos de proteção contra sobrecarga
- Molas de válvulas de taxa progressiva em motores de alto desempenho
- Molas cônicas em aplicações com restrição de espaço
3. Curva Característica Degressiva (Decrescente)
O oposto de progressivo, um curva característica degressiva ou decrescente Representa molas que se tornam mais macias à medida que são comprimidas. A curva começa íngreme e se achata.
Onde as molas regressivas se destacam:
- Absorção de impacto onde o impacto inicial precisa ser firmemente resistido.
- Certos tipos de aplicações de buffer
- Sistemas de amortecimento especializados
Curvas características combinadas e complexas
Aplicações do mundo real frequentemente exigem comportamentos de mola que não se encaixam perfeitamente nas três categorias básicas. É aí que entra o problema. curvas características combinadas entram em ação molas que exibem múltiplos comportamentos ao longo de sua faixa de atuação.
Fontes Volutas Cônicas
Molas de voluta cônica demonstram uma das características combinadas mais interessantes. Essas molas exibem:
- Fase Linear InicialNo início do carregamento, a mola se comporta de forma linear.
- Ponto de TransiçãoApós atingir uma determinada deflexão, a característica muda.
- Fase ProgressivaA mola fica cada vez mais rígida à medida que as espiras começam a chegar ao fim de sua extensão.
Esse comportamento torna as molas cônicas ideais para aplicações que exigem altura compacta (as espiras se encaixam umas dentro das outras), resistência progressiva controlada e alta capacidade de carga com uso eficiente do espaço.
Belleville (Disc) Springs
Fontes de Belleville As molas de disco são componentes fascinantes com curvas características únicas. Seu comportamento demonstra:
- Fase Degressiva InicialA mola começa com alta rigidez, que diminui...
- Transição intermediáriaUma região relativamente plana em algumas configurações.
- Fase Progressiva FinalA rigidez aumenta novamente à medida que a mola se aproxima do seu estado plano.
A curva geral geralmente forma um Em forma de S, tornando as molas Belleville incrivelmente versáteis para aplicações de alta carga e pequena deflexão, tensionamento e pré-carga de parafusos, compensação térmica em conjuntos e absorção de energia.
No Primavera de Cixi Díli, Fabricamos molas Belleville de precisão de acordo com padrões internacionais, incluindo a norma DIN 2093, atendendo aos requisitos exigentes de clientes em todo o mundo.
Molas de anel
Molas anulares exibem uma curva característica com significância histerese—as curvas de carga e descarga não seguem o mesmo caminho. Isso ocorre porque:
Em muitos conjuntos de molas anulares, a curva de carga pode parecer quase linear, enquanto a curva de descarga torna-se mais progressiva devido às perdas por atrito entre os elementos anulares.
- Durante o carregamento, o atrito entre os elementos do anel consome energia.
- A área entre as curvas de carga e descarga representa a dissipação de energia.
- Isso torna as molas anulares excelentes para amortecimento e absorção de vibrações.
Molas Combinadas
Molas combinadas Consistem em duas ou mais molas que trabalham juntas, geralmente molas de alturas diferentes dispostas em paralelo. Sua característica principal é:
- Fase de mola únicaInicialmente, apenas a mola mais alta suporta a carga — comportamento linear.
- Ponto de TransiçãoQuando a deflexão atinge o ponto de engate da mola mais curta
- Fase CombinadaAmbas as molas trabalham juntas, aumentando a taxa geral.
Entendendo a rigidez e a constante elástica de uma mola
Rigidez da mola, também chamado taxa de mola ou constante elástica, é um parâmetro fundamental que quantifica a resistência de uma mola à deformação. É definido como a razão entre o incremento de carga e o incremento de deflexão.

Figura 4: Fórmulas de rigidez de molas para molas de compressão/extensão e molas de torção
Resumo das fórmulas de rigidez:
Para molas de compressão e extensão:
F' = dF/df (N/mm ou lb/pol)
Para molas lineares: F' = F/f = constante (rigidez da mola k)
Para molas de torção:
T' = dT/dφ (N·mm/grau)
Para molas de torção lineares: T' = T/φ = constante
Rigidez Tangente vs. Rigidez Secante (Curvas Não Lineares)
Para molas não lineares, a "rigidez" depende da posição na curva. Dois valores são comumente usados em revisões de projeto e na comunicação com fornecedores:
- rigidez tangente (instantânea): a inclinação local em um ponto de trabalho, kt = dF/df
- rigidez secante (média): a linha da origem até esse ponto, ks = F/f
Em muitas referências, o deflexão estática/inicial fs é definida pela extensão do tangente em um ponto de operação até que ele intercepte o eixo de deflexão. Esta é uma maneira prática de "linearizar" localmente uma mola não linear em torno de um ponto de operação:
F ≈ kt × (f − fs)
Utilize essa aproximação apenas para pequenas variações em torno desse ponto de trabalho.
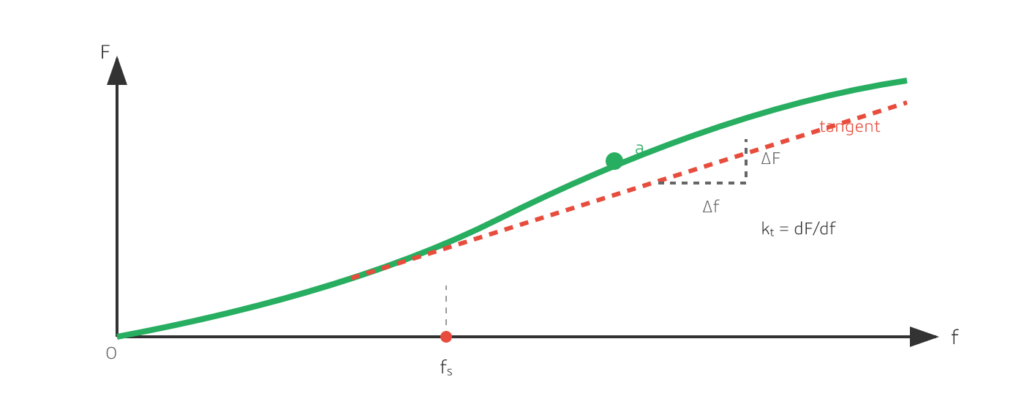
Figura 5: Em uma curva não linear, a rigidez depende do ponto de trabalho — rigidez tangente kt (dF/df) versus rigidez secante ks (F/f), mais deflexão estática/inicial fs.
Entendendo a Conformidade da Primavera
O inverso da rigidez é chamado conformidade ou flexibilidade. Representa a deformação produzida por unidade de força aplicada. A compliância é particularmente útil na análise de sistemas com múltiplas molas, no cálculo de deflexões a partir de cargas conhecidas e no projeto para requisitos específicos de flexibilidade.
Como as curvas características orientam a seleção de molas
Entender as curvas características não é apenas uma questão acadêmica — isso impacta diretamente na escolha da mola ideal para sua aplicação. Vamos explorar como diferentes curvas servem a propósitos distintos.
Molas Lineares: As Ferramentas Confiáveis para o Trabalho
Se a sua aplicação requer força previsível em qualquer posição, comportamento consistente em toda a faixa de trabalho e facilidade de cálculo e especificação, então as molas de característica linear são a melhor escolha.
Dica profissional: Ao especificar molas lineares, lembre-se de que a força em qualquer deflexão é simplesmente F = k × f. Isso torna o projeto do sistema simples e previsível.
Molas Progressivas: Início Suave, Finalização Firme
Aplicações que se beneficiam de características progressivas incluem:
Sistemas de suspensão de veículos: As suspensões automotivas modernas frequentemente utilizam molas progressivas com curvas em forma de S, pois em condições normais de condução, a taxa inicial mais macia proporciona uma viagem confortável, enquanto em curvas acentuadas ou ao passar por lombadas, a porção mais rígida é acionada para um controle preciso, e em condições extremas, a altura máxima da suspensão é atingida para evitar que a suspensão chegue ao fim do curso.
Curvas de histerese: Absorção de energia
Molas como as molas anulares, que apresentam histerese significativa, são escolhidas especificamente quando a energia precisa ser dissipada (e não armazenada e liberada), o amortecimento de vibrações é crucial e a absorção de impactos sem rebote é necessária.
Selecionando molas para sua aplicação: um guia prático.
Com base em nossas décadas de experiência em Primavera de Cixi Díli, Aqui está uma estrutura para selecionar molas com base em requisitos característicos:
| Tipo de aplicação | Característica recomendada | Tipos de molas |
|---|---|---|
| Força consistente ao longo de toda a faixa de atuação | Linear | Molas de compressão, extensão e matriz |
| Início suave, fim firme | Progressivo | Cônico, passo variável |
| Absorção de energia | Histerese | Molas de anel, conjuntos de molas de disco |
| Alta capacidade de carga, espaço pequeno | Varia | Belleville, Wave Springs |
| Resposta em dois estágios | Combinado | Molas Combinadas, Aninhadas |
Lista de verificação para solicitação de cotação (agiliza a elaboração de orçamentos): Compartilhe o tipo de mola e os pontos de funcionamento (por exemplo, F).1 @ f1, F2 @ f2), espaço de instalação disponível, deflexão máxima, requisito de taxa/curva (linear/progressiva/degressiva), meta de vida útil (ciclos), ambiente (temperatura/corrosão), tolerâncias, material, acabamento superficial e normas aplicáveis (JIS/DIN/ASTM, se houver).
Considerações práticas: da teoria à realidade
Embora as curvas características teóricas sejam calculadas usando modelos matemáticos, as molas do mundo real sempre apresentam algum desvio. Aqui está o que você precisa saber:
Tolerâncias de fabricação
Mesmo com a fabricação mais precisa — como os processos que usamos na Cixi Dili Spring Co., Ltd.—As variações ocorrem devido a variações nas propriedades do material (resistência ao escoamento, módulo de elasticidade), tolerâncias dimensionais (diâmetro do fio, diâmetro da bobina, passo), variações no tratamento térmico e efeitos do acabamento superficial.
Análise do setor: É por isso que aplicações críticas sempre exigem testes com amostras reais de molas. Na Dili Spring, podemos produzir molas de acordo com amostras ou desenhos do cliente e, em seguida, verificar o desempenho por meio de testes de carga para garantir que as curvas características atendam às especificações.
Efeitos da temperatura
A temperatura afeta significativamente o comportamento da mola: temperaturas mais altas geralmente reduzem a rigidez, a expansão térmica altera a geometria da mola e as propriedades do material (especialmente o módulo) variam com a temperatura. Para aplicações em altas temperaturas, a seleção adequada do material (como arame de aço para molas para temperaturas moderadas ou Inconel para calor extremo) é essencial.
Por que fazer parceria com um fabricante de molas experiente?
A complexidade das curvas características das molas e dos cálculos de rigidez ressalta a importância de trabalhar com fabricantes experientes. Veja o que Cixi Dili Spring Co., Ltd. traz para a mesa:
Suporte local + envio internacional: Sediados em Cixi (Ningbo), Zhejiang, China, oferecemos suporte a fabricantes de equipamentos originais (OEMs) em todo o mundo, com amostragem rápida e documentação pronta para exportação.
Três décadas de experiência: Desde 1995, fabricamos molas para clientes em todo o mundo, desenvolvendo profundo conhecimento em molas de matriz padrão JIS, molas de matriz padrão americanas, molas de torção, molas de compressão, molas de arame para instrumentos musicais, molas de extensão e molas com formatos personalizados para aplicações específicas.
Capacidades completas: Nosso sistema integrado de P&D, produção e vendas significa que entendemos a engenharia por trás de suas necessidades, podemos sugerir soluções ideais com base nas curvas características desejadas e mantemos um rigoroso controle de qualidade de acordo com os padrões internacionais.
Excelência em Personalização: Cada aplicação é única. Aceitamos projetos personalizados a partir de seus desenhos, engenharia reversa a partir de suas amostras e desenvolvimento colaborativo para novas aplicações.
Conclusão
As curvas características e a rigidez das molas são conceitos fundamentais que diferenciam aplicações de engenharia bem-sucedidas de problemáticas. Ao compreender os três tipos básicos de curvas — linear, progressiva e degressiva — e suas combinações, você adquire a capacidade de:
- Prever com precisão Comportamento de mola em seus aplicativos
- Selecione as molas ideais que correspondam exatamente às suas necessidades
- Solucionar problemas quando as molas não funcionam como esperado
- Comunique-se de forma eficaz. com fornecedores de molas sobre suas necessidades
Lembre-se: a curva característica conta toda a história de como uma mola irá se comportar. Seja para obter a consistência confiável de uma mola linear, a resposta sofisticada de uma mola progressiva automotiva ou as propriedades de absorção de energia de um sistema de molas anulares, compreender essas curvas é a chave para o sucesso.
Perguntas Frequentes (FAQs)
1. Qual a diferença entre taxa de mola e rigidez de mola?
Taxa de mola e rigidez da mola Essencialmente, são o mesmo conceito: ambos descrevem a força necessária para defletir uma mola por uma distância unitária (normalmente expressa em N/mm ou lb/in). Para molas lineares, esse valor é constante. Para molas não lineares, a "taxa" varia com a deflexão, portanto, geralmente nos referimos à taxa instantânea em um ponto de deflexão específico. Os termos são usados de forma intercambiável na indústria.
2. Uma única mola pode apresentar múltiplos comportamentos característicos de curva?
Sim, com certeza! Curvas características combinadas São bastante comuns. Uma mola de compressão de passo variável, por exemplo, começa com espiras mais macias que se fecham primeiro (comportamento linear) e, em seguida, passa a utilizar apenas espiras mais rígidas (comportamento progressivo). Conjuntos de molas de disco podem ser projetados para apresentar praticamente qualquer característica desejada, variando-se a disposição e o número de molas em série e em paralelo.
3. Como faço para medir a curva característica de uma mola existente?
Para medir a curva característica de uma mola, você precisará de um equipamento de teste de carga: monte a mola em um dispositivo de teste, aplique cargas crescentes incrementais, registre a deflexão em cada ponto de carga, plote os pontos de dados de carga-deflexão e conecte os pontos para revelar a curva característica. Para trabalhos de precisão, máquinas automatizadas de teste de molas podem gerar essas curvas de forma rápida e precisa.
4. Por que algumas molas apresentam curvas diferentes durante o carregamento e o descarregamento?
Esse fenômeno é chamado de histerese e ocorre devido às perdas de energia durante o funcionamento da mola. As causas incluem o atrito entre as espiras ou elementos da mola (especialmente em molas anulares e conjuntos de molas de disco), o amortecimento interno do material (mais significativo em molas de borracha ou polímero) e a interferência mecânica em certos projetos de molas. A área entre as curvas de carga e descarga representa a energia dissipada na forma de calor.
5. Como a temperatura afeta as curvas características de uma mola?
A temperatura afeta as molas de diversas maneiras: o módulo do material diminui em temperaturas mais altas (reduzindo a rigidez), a resistência ao escoamento se altera (afetando a capacidade máxima de carga), a expansão térmica modifica a geometria da mola e o relaxamento da tensão acelera em temperaturas elevadas. Para aplicações em altas temperaturas, a seleção do material é crucial. Molas de aço carbono padrão podem perder de 10 a 15% de sua constante elástica em temperaturas elevadas, enquanto ligas especiais como o Inconel mantêm suas propriedades muito melhor.
6. Qual a diferença entre rigidez secante (F/f) e rigidez tangente (dF/df)?
Em uma curva característica não linear, rigidez secante F/f é a taxa média da origem até um ponto, enquanto rigidez tangente dF/df é a inclinação instantânea no ponto de operação. Use a rigidez tangente para analisar pequenas variações em torno de um ponto de operação e a rigidez secante para estimativas rápidas em toda a faixa de valores.
Sobre a Cixi Dili Spring Co., Ltd.
Cixi Dili Spring Co., Ltd. Somos uma empresa de confiança na fabricação de molas desde 1995. Especializamo-nos na produção de molas de alta qualidade para clientes em todo o mundo, incluindo molas para matrizes (padrões JIS e americanos), molas de torção, molas de compressão, molas de extensão, molas de arame para instrumentos musicais e molas com formatos personalizados.
Nossa abordagem integrada — que abrange pesquisa e desenvolvimento, produção e vendas — garante que cada mola que entregamos atenda aos padrões internacionais e aos requisitos específicos de cada cliente.
Entre em contato conosco hoje mesmo:
E-mail: [email protected]
WhatsApp: +86 13586942004