Have you ever wondered why some springs feel “stiffer” as you compress them while others maintain a consistent resistance throughout their travel? Or why certain industrial applications require springs with very specific load-deflection behaviors? The answer lies in understanding spring characteristic curves and stiffness—two fundamental concepts that every engineer, designer, and procurement specialist should master.
In this comprehensive guide, we’ll dive deep into the science behind spring characteristic curves, explore the different types of curves and their practical implications, and help you understand how to select the right spring for your specific application. Whether you’re designing mold systems, automotive suspensions, or precision electronic devices, this knowledge will prove invaluable.
Quick Answer (60 seconds)
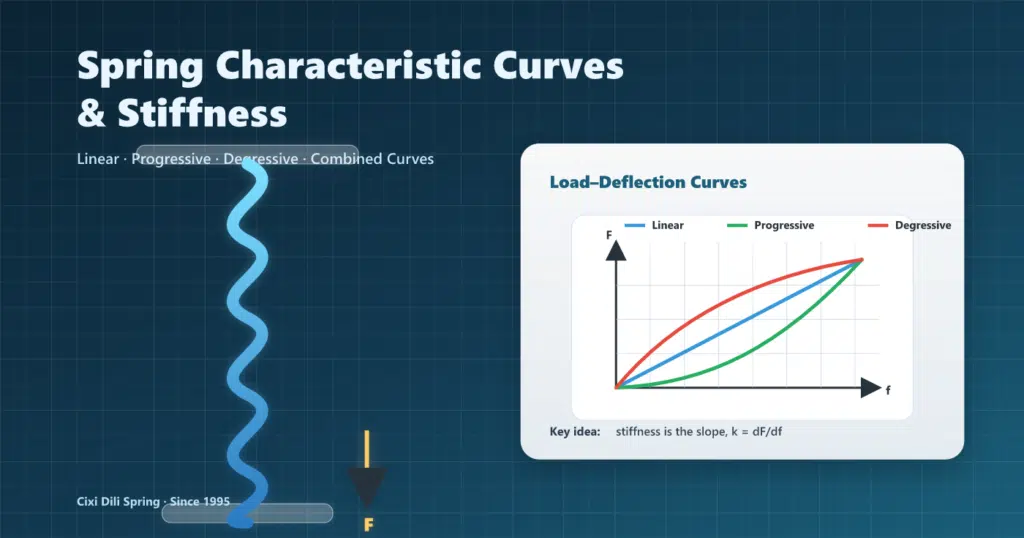
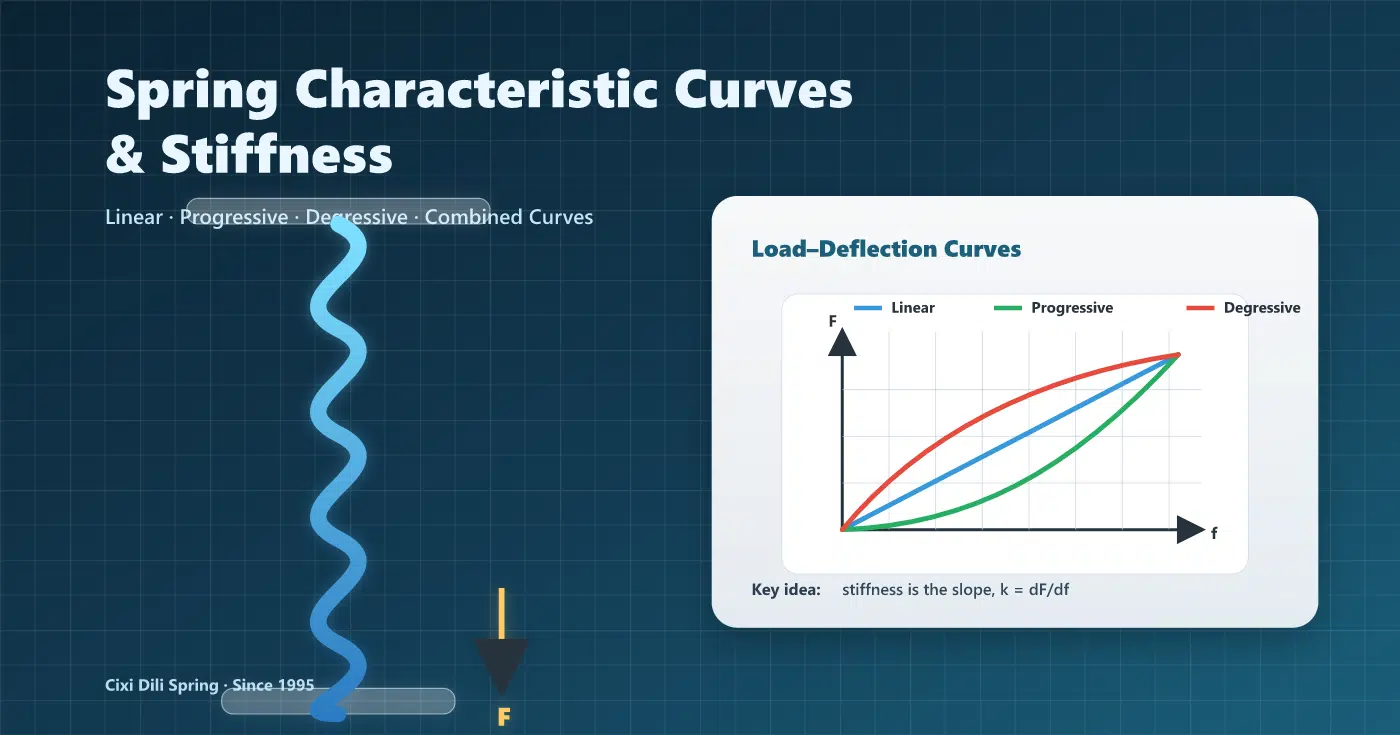
- Spring characteristic curve = the force–deflection (F–f) or torque–angle (T–φ) relationship.
- Stiffness / spring rate at a point is the curve slope: k = dF/df (or kθ = dT/dφ).
- Linear: k constant. Progressive: k increases with deflection. Degressive: k decreases with deflection.
- On non-linear curves, distinguish tangent stiffness (dF/df) vs secant stiffness (F/f) at the working point.
Table of Contents
- What Are Spring Characteristic Curves?
- Three Fundamental Curve Types
- Combined & Complex Curves
- Spring Stiffness & Spring Rate
- How Curves Guide Selection
- A Practical Selection Framework
- Practical Considerations
- Why Partner with a Manufacturer?
- Conclusion
- FAQs
What Are Spring Characteristic Curves?
A spring characteristic curve represents the relationship between the load (force F or torque T) applied to a spring and the resulting deformation (deflection f or angular displacement φ). Simply put, it’s a graphical representation of how a spring responds to increasing loads.
Think of it like this: if you push down on a spring with your hand and measure both the force you’re applying and how much the spring compresses, then plot those values on a graph, you’d create a characteristic curve. This curve tells the complete story of how that particular spring behaves under load.
Why Do Characteristic Curves Matter?
Understanding characteristic curves is crucial for several reasons:
- Predictable Performance: Engineers can accurately predict how a spring will perform in a given application
- Load Management: Knowing the curve helps in designing systems that manage loads effectively
- Safety Considerations: Critical applications require precise knowledge of spring behavior under extreme conditions
- Cost Optimization: Selecting the right spring type reduces overengineering and unnecessary costs
At Cixi Dili Spring Co., Ltd., we’ve been manufacturing springs since 1995, and we can tell you from experience that understanding these curves is often the difference between a successful application and a costly failure.
The Three Fundamental Types of Spring Characteristic Curves
Spring characteristic curves can be broadly categorized into three fundamental types, each with distinct behaviors and applications.
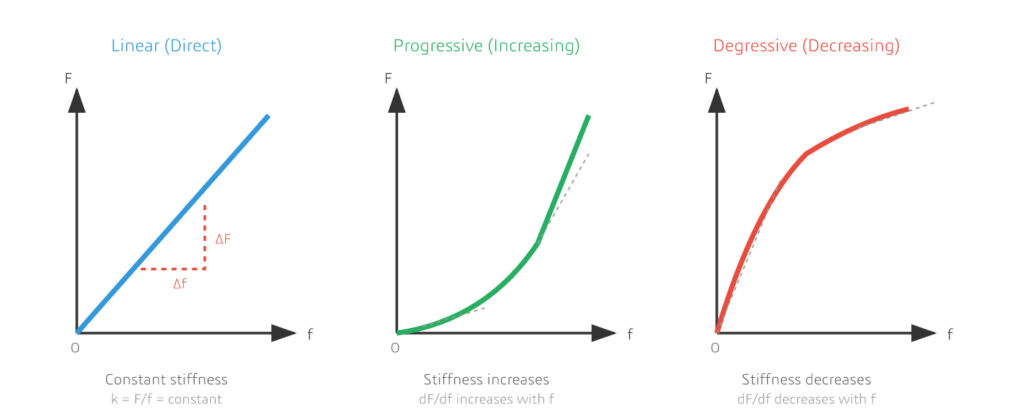
Figure 2: The three fundamental types of spring characteristic curves – Linear, Progressive (Increasing), and Degressive (Decreasing)
| Curve Type | What Happens to Stiffness (k) | Typical Designs | Best For |
|---|---|---|---|
| Linear | Constant: k = dF/df is the same across the working range | Most helical compression/extension springs, standard die springs | Predictable force at any position, easy sizing & control |
| Progressive | Increasing: k grows as deflection increases | Variable pitch, conical springs, designs that bring coils into contact | Soft initial response, overload/bottoming resistance |
| Degressive | Decreasing: k drops as deflection increases | Special geometries/material systems; some spring stacks | High initial resistance with softer follow-up response |
1. Linear Characteristic Curve
The linear characteristic curve is perhaps the most common and easiest to understand. In this type, the relationship between load and deflection is directly proportional—double the force, double the deflection.
Key Characteristics:
- The curve appears as a straight line on a load-deflection graph
- The spring rate (stiffness) remains constant throughout the working range
- Follows Hooke’s Law: F = k × f, where k is the spring constant
- Most helical compression and extension springs exhibit linear behavior
Where You’ll Find Linear Springs:
- Standard compression springs in everyday applications
- Extension springs in garage doors and trampolines
- Torsion springs in clothespins and mousetraps
- JIS and US standard die springs for consistent force application
Linear springs are the workhorses of the spring industry. When you need predictable, consistent performance without any surprises, linear characteristic springs are typically your best choice.
2. Progressive (Increasing) Characteristic Curve
A progressive or increasing characteristic curve shows a spring that becomes stiffer as it’s compressed or extended. The curve starts relatively flat and becomes steeper as deflection increases.
Mathematical Relationship:
For progressive springs, the relationship can be expressed as:
The rate of change dF/df increases as deflection f increases
This means F’/f > F/f at any point on the curve
Practical Applications:
- Automotive suspension systems requiring soft ride with firm bottoming resistance
- Overload protection mechanisms
- Progressive rate valve springs in high-performance engines
- Conical springs in space-constrained applications
3. Degressive (Decreasing) Characteristic Curve
The opposite of progressive, a degressive or decreasing characteristic curve represents springs that become softer as they’re compressed. The curve starts steep and flattens out.
Where Degressive Springs Excel:
- Shock absorption where initial impact needs to be firmly resisted
- Certain types of buffer applications
- Specialized damping systems
Combined and Complex Characteristic Curves
Real-world applications often require spring behaviors that don’t fit neatly into the three basic categories. This is where combined characteristic curves come into play—springs that exhibit multiple behaviors across their working range.
Conical Volute Springs
Conical volute springs demonstrate one of the most interesting combined characteristics. These springs exhibit:
- Initial Linear Phase: At the beginning of loading, the spring behaves linearly
- Transition Point: After reaching a certain deflection, the characteristic changes
- Progressive Phase: The spring becomes increasingly stiff as coils begin to bottom out
This behavior makes conical springs ideal for applications requiring compact solid height (coils nest inside each other), controlled progressive resistance, and space-efficient high-load capacity.
Belleville (Disc) Springs
Belleville springs or disc springs are fascinating components with unique characteristic curves. Their behavior shows:
- Initial Degressive Phase: The spring starts with high stiffness that decreases
- Middle Transition: A relatively flat region in some configurations
- Final Progressive Phase: Stiffness increases again as the spring approaches flat
The overall curve often forms an S-shape, making Belleville springs incredibly versatile for high-load, small-deflection applications, bolt tensioning and preloading, thermal compensation in assemblies, and energy absorption.
At Cixi Dili Spring, we manufacture precision Belleville springs to international standards including DIN 2093, meeting the exacting requirements of customers worldwide.
Ring Springs
Ring springs exhibit a characteristic curve with significant hysteresis—the loading and unloading curves don’t follow the same path. This is because:
In many ring spring assemblies, the loading curve can appear close to linear, while the unloading curve becomes more progressive due to frictional losses between ring elements.
- During loading, friction between ring elements consumes energy
- The area between loading and unloading curves represents energy dissipation
- This makes ring springs excellent for damping and vibration absorption
Combination Springs
Combination springs consist of two or more springs working together, often springs of different heights arranged in parallel. Their characteristic shows:
- Single Spring Phase: Initially, only the taller spring bears the load—linear behavior
- Transition Point: When deflection reaches the shorter spring’s engagement point
- Combined Phase: Both springs work together, increasing the overall rate
Understanding Spring Stiffness and Spring Rate
Spring stiffness, also called spring rate or spring constant, is a fundamental parameter that quantifies a spring’s resistance to deformation. It’s defined as the ratio of load increment to deflection increment.

Figure 4: Spring stiffness formulas for compression/extension springs and torsion springs
Stiffness Formulas Summary:
For Compression and Extension Springs:
F’ = dF/df (N/mm or lb/in)
For linear springs: F’ = F/f = constant (spring rate k)
For Torsion Springs:
T’ = dT/dφ (N·mm/degree)
For linear torsion springs: T’ = T/φ = constant
Tangent vs Secant Stiffness (Non-Linear Curves)
For non-linear springs, “stiffness” depends on where you are on the curve. Two values are commonly used in design reviews and supplier communication:
- Tangent (instantaneous) stiffness: the local slope at a working point, kt = dF/df
- Secant (average) stiffness: the line from the origin to that point, ks = F/f
In many references, the static/initial deflection fs is defined by extending the tangent at a working point until it intersects the deflection axis. This is a handy way to locally “linearize” a non-linear spring around an operating point:
F ≈ kt × (f − fs)
Use this approximation only for small variations around that working point.
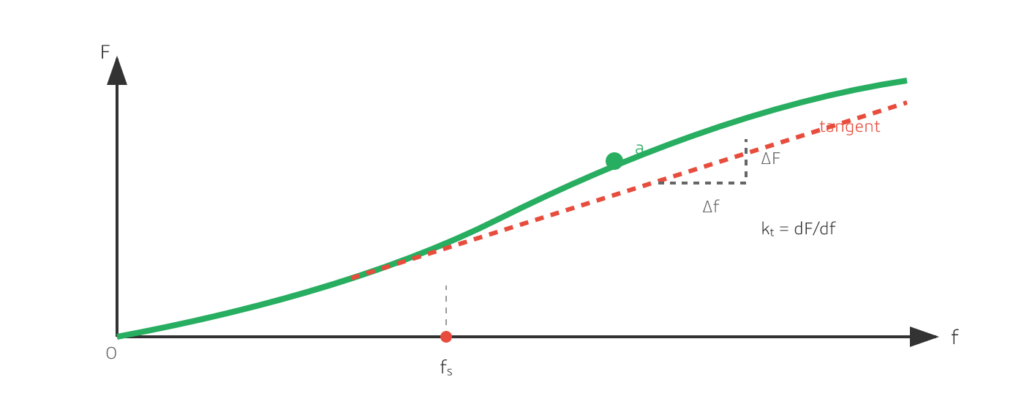
Figure 5: On a non-linear curve, stiffness depends on the working point—tangent stiffness kt (dF/df) vs secant stiffness ks (F/f), plus static/initial deflection fs.
Understanding Spring Compliance
The inverse of stiffness is called compliance or flexibility. It represents the deformation produced per unit of applied force. Compliance is particularly useful when analyzing systems with multiple springs, calculating deflections from known loads, and designing for specific flexibility requirements.
How Characteristic Curves Guide Spring Selection
Understanding characteristic curves isn’t just academic—it directly impacts which spring you should choose for your application. Let’s explore how different curves serve different purposes.
Linear Springs: The Reliable Workhorses
If your application requires predictable force at any position, consistent behavior throughout the working range, and easy calculation and specification, then linear characteristic springs are your best choice.
Pro Tip: When specifying linear springs, remember that the force at any deflection is simply F = k × f. This makes system design straightforward and predictable.
Progressive Springs: Soft Start, Firm Finish
Applications benefiting from progressive characteristics include:
Vehicle Suspension Systems: Modern automotive suspensions often use progressive springs with S-shaped curves because normal driving conditions engage the soft initial rate for a comfortable ride, hard cornering or bumps engage the stiffer portion for controlled handling, and extreme conditions approach the solid height for protection against bottoming.
Hysteresis Curves: Energy Absorption
Springs like ring springs that show significant hysteresis are specifically chosen when energy must be dissipated (not stored and released), vibration damping is critical, and impact absorption without rebound is required.
Selecting Springs for Your Application: A Practical Framework
Based on our decades of experience at Cixi Dili Spring, here’s a framework for selecting springs based on characteristic requirements:
| Application Type | Recommended Characteristic | Spring Types |
|---|---|---|
| Consistent force over range | Linear | Compression, Extension, Die Springs |
| Soft start, firm end | Progressive | Conical, Variable Pitch |
| Energy absorption | Hysteresis | Ring Springs, Disc Spring Stacks |
| High load, small space | Varies | Belleville, Wave Springs |
| Two-stage response | Combined | Combination Springs, Nested |
RFQ checklist (speeds up quoting): Share the spring type, working points (e.g., F1 @ f1, F2 @ f2), available installation space, maximum deflection, rate/curve requirement (linear/progressive/degressive), life target (cycles), environment (temperature/corrosion), tolerances, material, surface finish, and applicable standards (JIS/DIN/ASTM if any).
Practical Considerations: From Theory to Reality
While theoretical characteristic curves are calculated using mathematical models, real-world springs always show some deviation. Here’s what you need to know:
Manufacturing Tolerances
Even with the most precise manufacturing—like the processes we use at Cixi Dili Spring Co., Ltd.—variations occur due to material property variations (yield strength, modulus), dimensional tolerances (wire diameter, coil diameter, pitch), heat treatment variations, and surface finish effects.
Industry Insight: This is why critical applications always require testing actual spring samples. At Dili Spring, we can produce springs to customer samples or drawings, then verify performance through load testing to ensure characteristic curves meet specifications.
Temperature Effects
Temperature significantly affects spring behavior: higher temperatures generally reduce stiffness, thermal expansion changes spring geometry, and material properties (especially modulus) vary with temperature. For high-temperature applications, proper material selection (like music wire for moderate temperatures or Inconel for extreme heat) is essential.
Why Partner with an Experienced Spring Manufacturer?
The complexities of spring characteristic curves and stiffness calculations underscore the importance of working with knowledgeable manufacturers. Here’s what Cixi Dili Spring Co., Ltd. brings to the table:
Local support + global shipping: Based in Cixi (Ningbo), Zhejiang, China, we support OEMs worldwide with fast sampling and export-ready documentation.
Three Decades of Expertise: Since 1995, we’ve been manufacturing springs for global customers, developing deep expertise in JIS standard die springs, US standard die springs, torsion springs, compression springs, music wire springs, extension springs, and custom-shaped springs for unique applications.
Complete Capabilities: Our integrated R&D, production, and sales system means we understand the engineering behind your requirements, can suggest optimal solutions based on characteristic curve needs, and maintain strict quality control to international standards.
Customization Excellence: Every application is unique. We welcome custom designs from your drawings, reverse engineering from your samples, and collaborative development for new applications.
Conclusion
Spring characteristic curves and stiffness are foundational concepts that separate successful engineering applications from problematic ones. By understanding the three basic curve types—linear, progressive, and degressive—and their combinations, you gain the ability to:
- Accurately predict spring behavior in your applications
- Select optimal springs that match your exact requirements
- Troubleshoot problems when springs don’t perform as expected
- Communicate effectively with spring suppliers about your needs
Remember, the characteristic curve tells the complete story of how a spring will behave. Whether you need the reliable consistency of a linear die spring, the sophisticated response of a progressive automotive spring, or the energy-absorbing properties of a ring spring system, understanding these curves is your key to success.
Frequently Asked Questions (FAQs)
1. What is the difference between spring rate and spring stiffness?
Spring rate and spring stiffness are essentially the same concept—both describe the force required to deflect a spring by a unit distance (typically expressed in N/mm or lb/in). For linear springs, this is a constant value. For non-linear springs, the “rate” varies with deflection, so we typically reference the instantaneous rate at a specific deflection point. The terms are used interchangeably in the industry.
2. Can a single spring have multiple characteristic curve behaviors?
Yes, absolutely! Combined characteristic curves are quite common. A variable-pitch compression spring, for example, starts with softer coils that close first (linear behavior), then transitions to stiffer coils only (progressive behavior). Disc spring stacks can be designed to exhibit almost any desired characteristic by varying the arrangement and number of springs in series and parallel.
3. How do I measure the characteristic curve of an existing spring?
To measure a spring’s characteristic curve, you’ll need load testing equipment: mount the spring in a test fixture, apply incrementally increasing loads, record the deflection at each load point, plot the load-deflection data points, and connect the points to reveal the characteristic curve. For precision work, automated spring testing machines can generate these curves quickly and accurately.
4. Why do some springs show different curves during loading versus unloading?
This phenomenon is called hysteresis and occurs due to energy losses during the spring’s operation. The causes include friction between coils or spring elements (especially in ring springs and disc spring stacks), internal material damping (more significant in rubber or polymer springs), and mechanical interference in certain spring designs. The area between loading and unloading curves represents energy dissipated as heat.
5. How does temperature affect spring characteristic curves?
Temperature affects springs in several ways: material modulus decreases at higher temperatures (reducing stiffness), yield strength changes (affecting maximum load capacity), thermal expansion alters spring geometry, and stress relaxation accelerates at elevated temperatures. For high-temperature applications, material selection is critical. Standard carbon steel springs may lose 10-15% of their rate at elevated temperatures, while specialty alloys like Inconel maintain properties much better.
6. What’s the difference between secant stiffness (F/f) and tangent stiffness (dF/df)?
On a non-linear characteristic curve, secant stiffness F/f is the average rate from the origin to a point, while tangent stiffness dF/df is the instantaneous slope at the working point. Use tangent stiffness to analyze small variations around an operating point, and secant stiffness for quick across-the-range estimates.
About Cixi Dili Spring Co., Ltd.
Cixi Dili Spring Co., Ltd. has been a trusted name in spring manufacturing since 1995. We specialize in producing high-quality springs for global customers, including die springs (JIS & US standard), torsion springs, compression springs, extension springs, music wire springs, and custom-shaped springs.
Our integrated approach—covering R&D, production, and sales—ensures that every spring we deliver meets international standards and customer-specific requirements.
Contact Us Today:
Email: [email protected]
WhatsApp: +86 13586942004